マイコン君　Ｅ資格の勉強メモ（その２）

（第１回）ベクトルと行列の内積

機械学習のメモ（その２）では、自然言語処理をメインに調べていきます。まずは、重要なベクトルと行列について、再度調べてみようと思います。

＜ベクトル・行列＞

ベクトルは、１次の行列で縦、横のベクトルで表現されます。主に２次の行列（複数行）で表現されます。

縦ベクトル・・・$\large{\begin{bmatrix}1 \\2 \\3 \end{bmatrix}} $

横ベクトル・・・$\large{\begin{bmatrix}1 & 2 & 3 \end{bmatrix}}$

行列・・・$\large{\begin{bmatrix}1 & 2 \\3 & 4 \\5 & 6 \end{bmatrix}}$

＜アダーマール積・内積＞

〇アダマール積

各成分をそれぞれ掛け算する方法になります。

$\large{A=\begin{bmatrix}a1 & a2 \\a3 & a4 \end{bmatrix}}$ $\large{B=\begin{bmatrix}b1 & b2 \\b3 & b4 \end{bmatrix}}$
$\large{A×B=\begin{bmatrix}a1×b1 & 　　a2×b2 \\a3×b3 & 　　a4×b4 \end{bmatrix}}$
となります。

〇内積

線形代数の行列の基本の計算になります。

$\large{A=\begin{bmatrix}a1 & a2 \\a3 & a4 \end{bmatrix}}$ $\large{B=\begin{bmatrix}b1 & b2 \\b3 & b4 \end{bmatrix}}$
$\large{A・B=\begin{bmatrix}a1×b1＋a2×b3 & 　　a1×b2＋a2×b4　 \\a3×b1＋a4×b2 & 　　a3×b2＋a4×b4　\end{bmatrix}}$
となります。ＡＢが２ｘ２の行列ですので、問題ないですが、Ａが２Ｘ３の場合、必ずＢは３ｘ〇の行列である必要があり、対応する次元の要素数を一致させる必要があります。

Ｐｙｔｈｏｎでプログラムを書くと以下のようになります。

import numpy as np
a=np.array([[1,2],[3,4]])
b=np.array([[1,2],[3,4]])
print('アダマール積')
print(a*b)
print('内積')
print(np.dot(a,b))

結果

アダマール積
[[ 1  4]
 [ 9 16]]
内積
[[ 7 10]
 [15 22]]

基本的には、内積を使います。内積は掛け算の順番を変更すると結果が変わります。
行列の積を利用することで、機械学習ではいろいろな計算を実施できるので、便利です。

＜Ｓｉｇｍｏｉｄ関数＋ミニバッチ＞

入力のデータを複数個まとめて処理してみます。複数個まとめてあるデータをミニバッチと言います。
まずは、活性関数である、シグモイド関数

$\large{σ(x)=\frac{1}{1+exp(-x)}}$

これをニューロン：ｈ＝ｗｘ＋ｂ（ｗ：重み、ｘ：入力、ｂ：バイアス）を考慮して、Ｐｙｔｈｏｎで計算します。
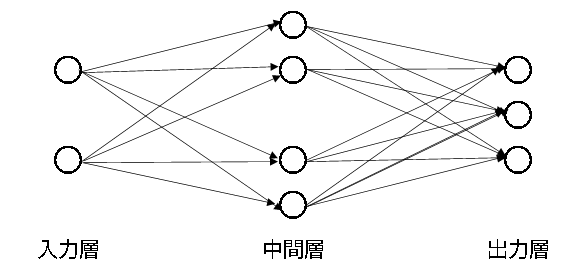
ミニバッチは１０個、入力は２次元、中間層は４次元(Sigmoid)、出力は３次元とします。(上のネットワークが１０組ある。)
以下がプログラムです。

import numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))

x=np.random.randn(10,2)
w1=np.random.randn(2,4)
b1=np.random.randn(4)
w2=np.random.randn(4,3)
b2=np.random.randn(3)

h=np.dot(x,w1)+b1
a=sigmoid(h)
s=np.dot(a,w2)+b2

print('入力（ｘ）')
print(x)
print('中間層１層目重さ（ｗ１）')
print(w1)
print('中間層１層目バイアス（ｂ１）')
print(b1)
print('中間層２層目重さ（ｗ２）')
print(w2)
print('中間層２層目バイアス（ｂ２）')
print(b2)

print('ｈ＝ｘｗ１＋ｂ１')
print(h)
print('ａ＝ｓｉｇｍｏｉｄ（ｈ）')
print(a)
print('ｓ＝ａｗ２＋ｂ２')
print(s)

結果

入力（ｘ）
[[-1.22159838  0.86769414]
 [-0.9479115   0.92195912]
 [-0.95538335  2.52724699]
 [-0.92197832 -0.77697841]
 [ 0.10054629 -1.53882293]
 [-0.12038797  3.05817932]
 [ 0.32683089  0.38716539]
 [-0.40996935  0.75989205]
 [-1.16730835  0.14332013]
 [-1.78343517 -0.95828207]]
中間層１層目重さ（ｗ１）
[[-1.5831248   0.50423533  1.59311436  1.15409987]
 [-0.07289595  1.0634004   1.1888912   1.06355459]]
中間層１層目バイアス（ｂ１）
[ 1.87682152 -1.05664709 -0.82548395 -0.94502798]
中間層２層目重さ（ｗ２）
[[ 2.92816493 -1.10607406 -1.09368946]
 [ 1.1370407  -1.29661307 -0.12299486]
 [ 1.24690001  1.72043249 -0.33567739]
 [-0.84355248  0.04682903 -1.58670843]]
中間層２層目バイアス（ｂ２）
[-0.81569095 -1.01602258 -1.01232382]
ｈ＝ｘｗ１＋ｂ１
[[ 3.74751283 -0.74991384 -1.74003594 -1.43203443]
 [ 3.31027665 -0.55420585 -1.23950629 -1.05845867]
 [ 3.20508652  1.14909035  0.65710283  0.64022936]
 [ 3.39306685 -2.34778028 -3.21804364 -2.835442  ]
 [ 1.82981816 -2.64233303 -2.49479526 -2.46560972]
 [ 1.84448181  2.13471817  2.61856673  2.16857293]
 [ 1.33118464 -0.48013558  0.15549255 -0.15606097]
 [ 2.47046111 -0.4552986  -0.57518303 -0.60998687]
 [ 3.71436887 -1.49283851 -2.5147476  -2.13978962]
 [ 4.77007686 -2.97495565 -4.80599324 -4.02247558]]
ａ＝ｓｉｇｍｏｉｄ（ｈ）
[[0.97696673 0.32084007 0.14930837 0.19278189]
 [0.96477968 0.36488917 0.22452194 0.25760411]
 [0.96102524 0.75934473 0.65860928 0.65480531]
 [0.96748715 0.08724237 0.03849233 0.05543874]
 [0.86174006 0.06646313 0.07622386 0.07830451]
 [0.8634779  0.89423209 0.93204699 0.89739164]
 [0.79103652 0.38222011 0.538795   0.46106375]
 [0.92204491 0.38810172 0.36004173 0.35206219]
 [0.97620899 0.18349606 0.07483076 0.10528921]
 [0.99159157 0.0485702  0.00811419 0.0175935 ]]
ｓ＝ａｗ２＋ｂ２
[[ 2.43338794 -2.24672281 -2.47629182]
 [ 2.48689073 -2.15792224 -2.59648225]
 [ 3.1306126  -1.89980727 -3.41684785]
 [ 2.11769972 -2.13043502 -2.1820708 ]
 [ 1.81218693 -1.92054295 -2.11280752]
 [ 3.13466549 -1.48501821 -3.80345243]
 [ 2.21808629 -1.43800755 -2.83691828]
 [ 2.47744918 -1.90317608 -2.74796707]
 [ 2.25594197 -2.20003354 -2.29474465]
 [ 2.13835555 -2.16098925 -2.13343047]]

入力には、行列（１０ｘ２）のミニバッチ、ｗ１，ｂ１の１層目を計算すると、行列（１０ｘ４）になっています。ｓｉｇｏｍｏｉｄもそのまま行列（１０ｘ４）のミニバッチのまま計算できていて、ｗ２，ｂ２で出力層を計算していますが、行列（１０ｘ３）のデータとして出力ができています。
エクセルなどで計算する場合For文で繰り返し計算させることがありますが、それがＮｕｍｐｙの行列計算では１度の計算できています。

－－－－－－－－－－－－－