マイコン君　Ｅ資格の勉強メモ（その２）

（第２回）ニューラルネットワーク

自然言語処理でもニューラルネットワークを利用して進めます。ＭＮＩＳＴでは基本的な部分から始めましたが、今回はレイヤを利用して、まとめてみます。

＜２層　ニューラルネットワーク＞

レイヤを利用して２層のニューラルネットワークをＰｙｔｈｏｎで作成します。

第１回と同じ構成ですが、クラスを利用して呼び出す事で、複雑になっても理解しやすくなっています。

# coding: utf-8
import numpy as np


class Sigmoid:
    def __init__(self):
        self.params = []

    def forward(self, x):
        return 1 / (1 + np.exp(-x))


class Affine:
    def __init__(self, W, b):
        self.params = [W, b]

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        return out


class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size):
        I, H, O = input_size, hidden_size, output_size

        # 重みとバイアスの初期化
        W1 = np.random.randn(I, H)
        b1 = np.random.randn(H)
        W2 = np.random.randn(H, O)
        b2 = np.random.randn(O)

        # レイヤの生成
        self.layers = [
            Affine(W1, b1),
            Sigmoid(),
            Affine(W2, b2)
        ]

        # すべての重みをリストにまとめる
        self.params = []
        for layer in self.layers:
            self.params += layer.params

    def predict(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x


x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
print('入力（ｘ）')
print(x)
print('中間層１層目重さ（ｗ１）')
print(model.params[0])
print('中間層１層目バイアス（ｂ１）')
print(model.params[1])
print('中間層２層目重さ（ｗ２）')
print(model.params[2])
print('中間層２層目バイアス（ｂ２）')
print(model.params[3])
print('出力')
print(s)

同じような出力が得られます。順伝播のみがプログラムされていますが、今後、逆伝播が不可欠になってくるので、このプログラムの方が効率よく処理が可能です。

$\large{X→\begin{bmatrix}　\\Affine \\　\end{bmatrix}→\begin{bmatrix}　\\Sigmoid \\　\end{bmatrix}→\begin{bmatrix}　\\Affine \\　\end{bmatrix}→S}$

上記がレイヤの構成になります。２層のニューラルネットワークですが、レイヤが３個あるので、入力～出力の間に３つのレイヤがあることを表しています。

＜２層　ニューラルネットワーク＋損失関数＞

２層のニューラルネットワークに損失関数を接続します。損失は最適なパラメータを推測するために現状のパラメーターがどうなのか？評価するために重要な関数になります。
プログラムを書いてみます。

# coding: utf-8
import numpy as np


class Sigmoid:
    def __init__(self):
        self.params = []

    def forward(self, x):
        return 1 / (1 + np.exp(-x))


class Affine:
    def __init__(self, W, b):
        self.params = [W, b]

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        return out


class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size):
        I, H, O = input_size, hidden_size, output_size

        # 重みとバイアスの初期化
        W1 = np.random.randn(I, H)
        b1 = np.random.randn(H)
        W2 = np.random.randn(H, O)
        b2 = np.random.randn(O)

        # レイヤの生成
        self.layers = [
            Affine(W1, b1),
            Sigmoid(),
            Affine(W2, b2)
        ]

        # すべての重みをリストにまとめる
        self.params = []
        for layer in self.layers:
            self.params += layer.params

    def predict(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x
    

def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)   # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)  
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if t.size == y.size:
        t = t.argmax(axis=1)
             
    batch_size = y.shape[0]
    #return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size,t#合計する
    return -np.log(y[np.arange(batch_size), t] + 1e-7) / batch_size,t#個別出力る

t = np.random.randn(10, 3)
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
y = softmax(s)

L = cross_entropy_error(y,t)
print('正解')
print(t)
print('入力（ｘ）')
print(x)
print('中間層１層目重さ（ｗ１）')
print(model.params[0])
print('中間層１層目バイアス（ｂ１）')
print(model.params[1])
print('中間層２層目重さ（ｗ２）')
print(model.params[2])
print('中間層２層目バイアス（ｂ２）')
print(model.params[3])
print('出力')
print(s)
print('Softmax')
print(y)
print('正解ラベル')
print(L[1])
print('損失関数')
print(L[0])

結果

正解
[[-0.29830205 -1.10291417  0.83481792]
 [ 0.10825548 -0.69970388 -0.35544306]
 [-1.05421816  0.35514705  1.21975282]
 [-0.07268953  0.68632447  0.06417656]
 [ 1.25637497 -0.13130044  0.48222075]
 [ 0.67036417 -0.39678665  1.83657672]
 [-0.68640472 -1.00550081 -0.85462817]
 [ 0.80342954 -0.47344461 -1.26538788]
 [ 0.53882519  0.09093636  0.03546234]
 [-1.33891416  0.50340027  0.77509397]]
入力（ｘ）
[[ 1.13549484  1.61953034]
 [ 0.14602155  1.58135775]
 [-0.7684719   1.58954177]
 [ 1.03760285 -0.98833757]
 [-1.16824654 -0.06787699]
 [ 0.82769173  0.83222598]
 [ 1.9493354   0.83275075]
 [ 0.54884354 -0.89347842]
 [-1.63383831 -2.62982454]
 [-0.4936866  -2.28138098]]
中間層１層目重さ（ｗ１）
[[-0.0895282   1.26699632  0.34052469 -0.44706338]
 [-0.87990036  0.43760064  1.06715259 -0.46415335]]
中間層１層目バイアス（ｂ１）
[-1.24469477  1.75976365 -0.18895627  0.17173643]
中間層２層目重さ（ｗ２）
[[-0.30657364  0.27191755  0.28356089]
 [ 1.4751231  -0.25683613  0.4284283 ]
 [-1.26777482 -1.21889931  1.05638017]
 [ 0.74975269 -1.46535208 -0.69752419]]
中間層２層目バイアス（ｂ２）
[ 0.50257643  1.51308773 -0.73573449]
出力
[[ 1.01305063 -0.15590531  0.44714257]
 [ 1.07437204 -0.22386702  0.31117582]
 [ 1.03170387 -0.27496997  0.14364089]
 [ 1.79861477  0.22972673 -0.29689007]
 [ 1.32711524  0.03468993 -0.53289755]
 [ 1.22971394 -0.11337384  0.22646026]
 [ 1.11061459 -0.05324451  0.38316346]
 [ 1.78240702  0.19234446 -0.3632509 ]
 [ 1.17814719  0.33176788 -1.02986963]
 [ 1.61241688  0.3063086  -0.8150208 ]]
Softmax
[[0.53232959 0.16539009 0.30228031]
 [0.57498157 0.15697694 0.26804149]
 [0.59446989 0.1609343  0.24459581]
 [0.75115409 0.15644786 0.09239806]
 [0.69916643 0.19199388 0.10883969]
 [0.61435521 0.1603703  0.22527449]
 [0.55697348 0.17393098 0.26909554]
 [0.75705735 0.15437372 0.08856893]
 [0.64982169 0.27875094 0.07142737]
 [0.73576216 0.19929749 0.06494035]]
正解ラベル
[2 0 2 1 0 2 0 0 0 2]
損失関数
[0.11964002 0.05534171 0.14081478 0.18550319 0.03578663 0.14904352
 0.05852375 0.02783161 0.04310571 0.27342845]

損失関数が追加されていますが、出力が３次元なので、正解ラベルは、行列（１０ｘ３）から１０個の０～２のラベルに変換されます。１０個のランダムデータですが、損失関数は入力の最大と同じ要素が正解の場合は、値が小さく、不正解の場合は大きくなっていることがわかります。

$X→\begin{bmatrix}　\\Affine \\　\end{bmatrix}→\begin{bmatrix}　\\Sigmoid \\　 \end{bmatrix}→\begin{bmatrix}　\\Affine \\　\end{bmatrix}→\begin{bmatrix}　\\Softmax \\　 \end{bmatrix}＊）→\begin{bmatrix}Cross　\\Entropy \\Error　\end{bmatrix}→L$
*)正解ラベルの追加位置：　$t→$
上記がレイヤの構成になります。

＜計算グラフ＞

ニューラルネットワークの学習をする場合、順伝播と逆伝播を計算して、パラメーター（重み、バイアス）を変更します。順伝播で微分をして勾配を求めながら、パラメーターを変更することもできますが、計算負荷が大きすぎるため、現実的ではありません。
順伝播と逆伝播を理解するために、計算グラフを用いると理解がしやすいため、調べていきます。

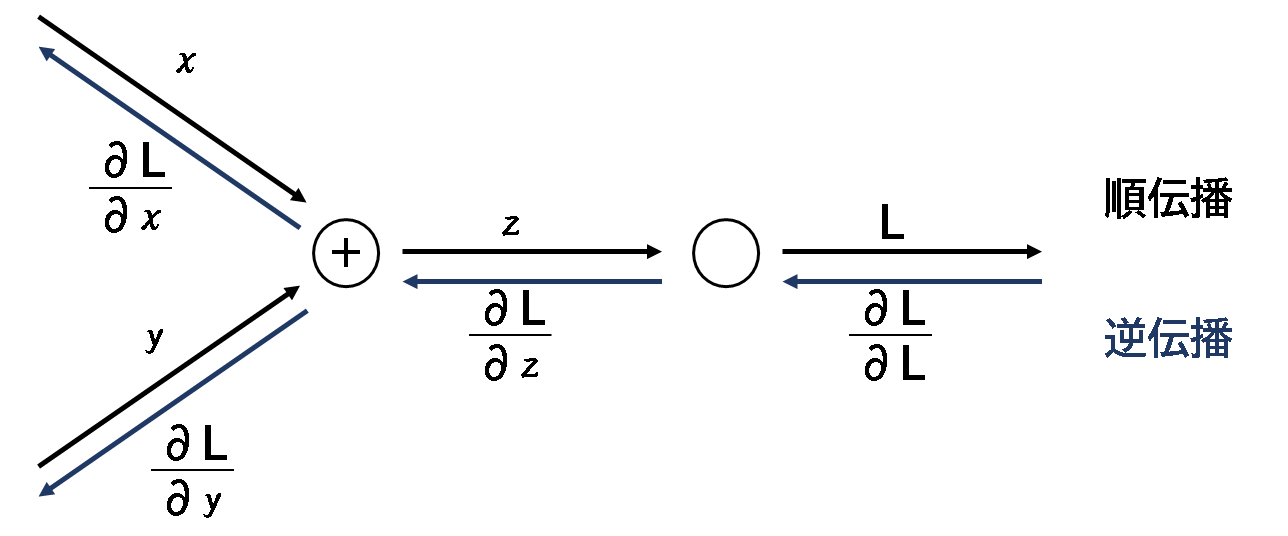
＜ノード①＞

加算、乗算、分岐ノードについてです。加算は、出力をそのまま戻す形、乗算は、出力に順伝播の入力を入れ替えて、分岐は、分岐した物を足し算するような方法でそれぞれ逆伝播します。分岐ノードはコピーノードとも言うそうです。

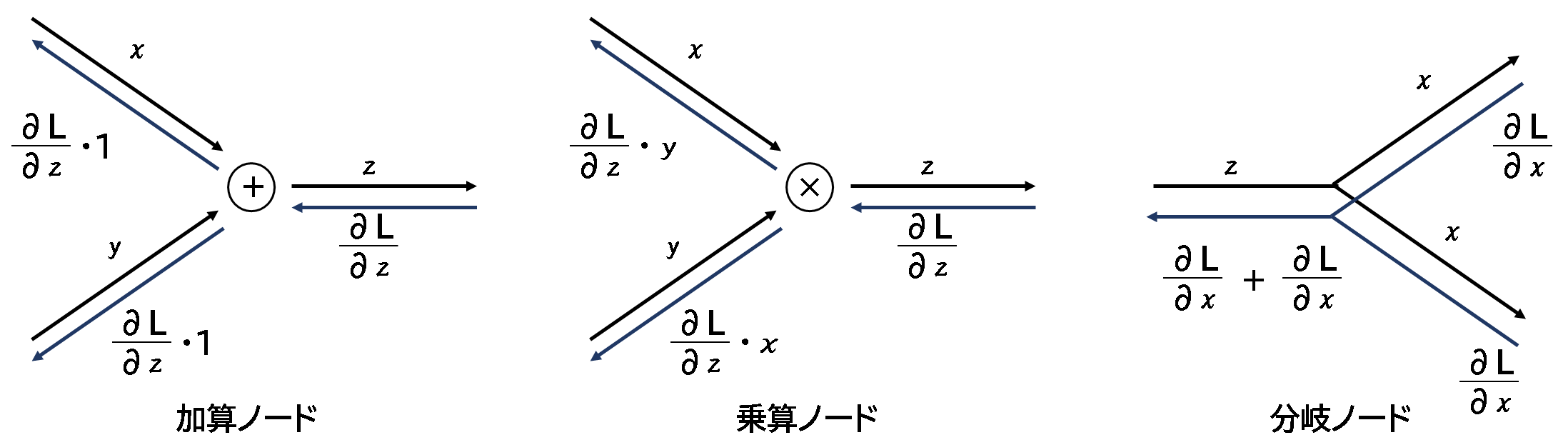
＜ノード②＞

分岐は１個だけでしたが、複数に対応したRepeatノード、Sumノードを見てみます。順伝播、逆伝播とも同じ列数ですが、 Repeatは１→Ｎ行へ分岐（コピー）、SumはＮ→１行への加算（集約）がされていることが特徴的です。

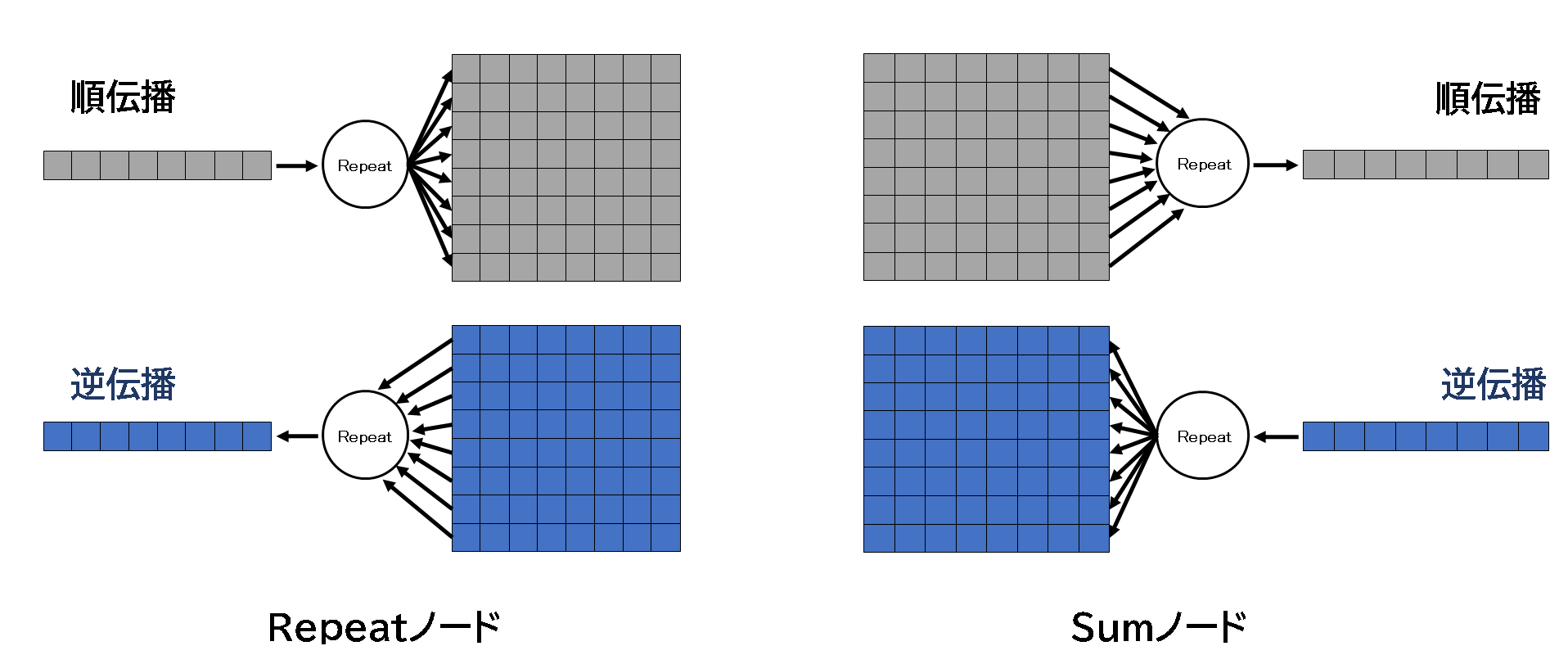
Ｐｙｔｈｏｎで書くと以下のとおりになります。

# coding: utf-8
import numpy as np

D,N =8,7

print('Repeatノード')

print('順伝播')
print('入力')
x=np.random.randn(1,D)
print(x)
print('出力')
y=np.repeat(x,N,axis=0)
print(y)
print('逆伝播')
print('入力')
dy=np.random.randn(N,D)
print(dy)
print('出力')
dx=np.sum(dy,axis=0,keepdims=True)
print(dx)
print(' ')
print('Sumノード')
print('順伝播')
print('入力')
x=np.random.randn(N,D)
print(x)
print('出力')
y=np.sum(x,axis=0,keepdims=True)
print(y)
print('逆伝播')
print('入力')
dy=np.random.randn(1,D)
print(dy)
print('出力')
dx=np.repeat(dy,N,axis=0)
print(dx)
#keepdims=True ２次配列保持

出力を確認すると、図のように順伝播、逆伝播が表示されています。keepdims=Trueは２次配列保持。axis=0は行方向の分岐(repeat)や総和(sum)を求める形になります。

＜ノード③＞

行列の積をＭａｔＭａｌノードという形で計算します。形状は以下のとおりで、順伝播、逆伝播次の式で計算されます。

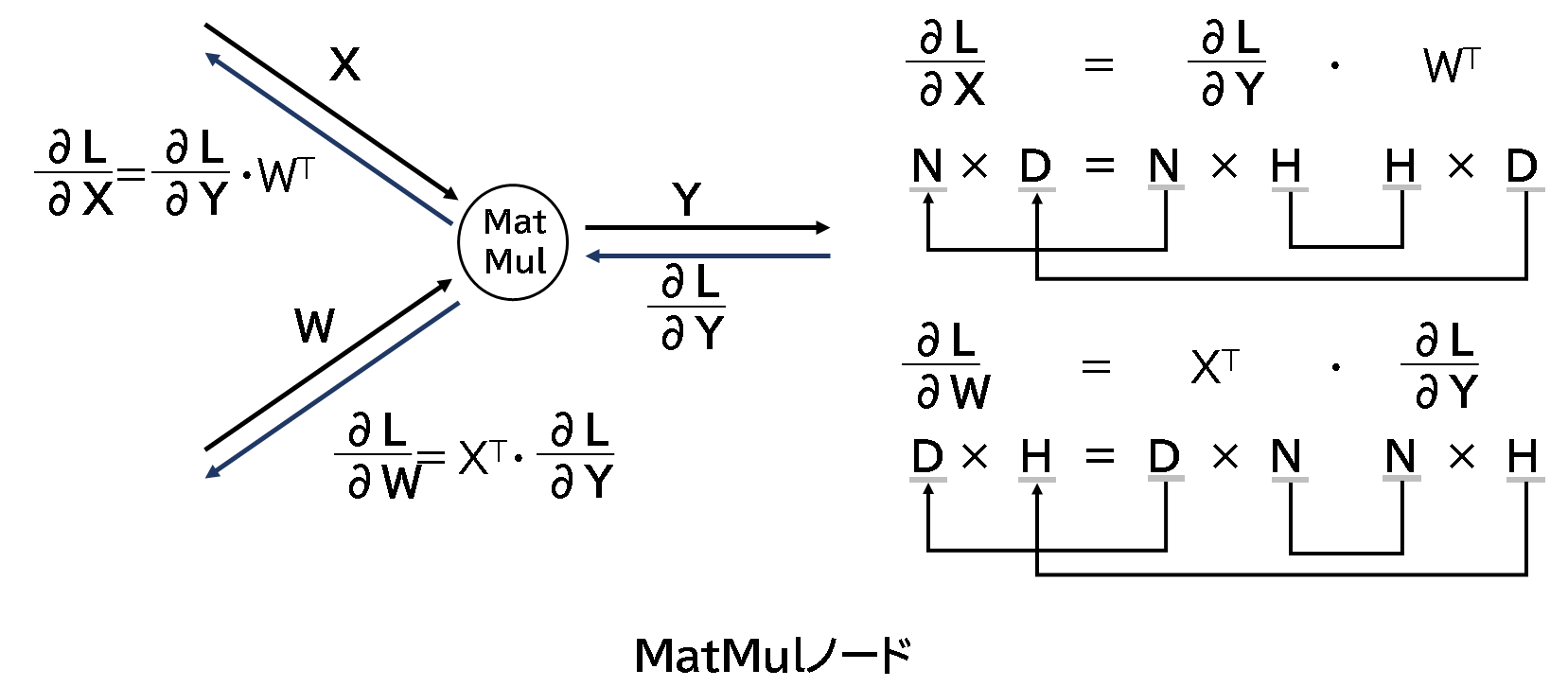
Ｐｙｔｈｏｎで書くと以下のとおりになります。

# coding: utf-8
import numpy as np

class MatMul:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.x = None

    def forward(self, x):
        W, = self.params
        out = np.dot(x, W)
        self.x = x
        return out

    def backward(self, dout):
        W, = self.params
        dx = np.dot(dout, W.T)
        dW = np.dot(self.x.T, dout)
        self.grads[0][...] = dW#メモリの位置もコピーされる
        return dW,dx

N,D,H =5,2,3#N：データの個数、D：入力ノード数、H：隠れ層の数

print('MatMulノード')

print('順伝播')
print('X')
x=np.random.randn(N,D)
print(x)
print('W')
w=np.random.randn(D,H)
print(w)
MatMul_Model=MatMul(w)
MatMul_Model_F=MatMul_Model.forward(x)

print('Y')
y=MatMul_Model_F
print(y)

print('逆伝播')
print('dx')
MatMul_Model_B=MatMul_Model.backward(MatMul_Model_F)
RetuenVal=MatMul_Model_B
print(RetuenVal[1])
print('dw')
print(RetuenVal[0])

入力Ｘと重みＷの行列の積を順伝播で出力して、そのまま逆伝播でｄｘ，ｄｗを表示させています。同じ形状の行列が逆伝播の戻り値が得られています。

＜Ａｆｆｉｎｅレイヤ＞

ＭａｔＭａｌ、Ｒｅｐｅａｔノードを使うと以下のようにＡｆｆｉｎｅレイヤを計算グラフで表すことができます。

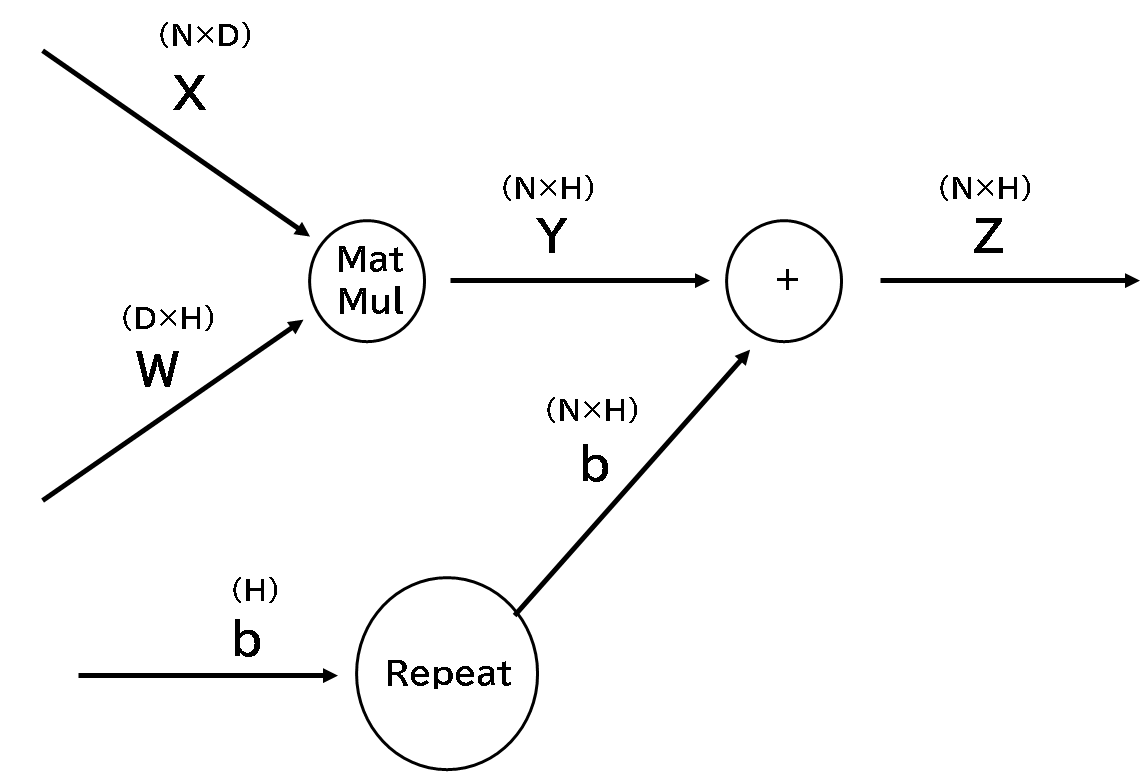
Ｐｙｔｈｏｎで書くと以下のとおりになります。

# coding: utf-8
import numpy as np

class Affine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        self.x = x
        return out

    def backward(self, dout):
        W, b = self.params
        dx = np.dot(dout, W.T)
        dW = np.dot(self.x.T, dout)
        db = np.sum(dout, axis=0)

        self.grads[0][...] = dW
        self.grads[1][...] = db
        return dW,dx

N,D,H =5,2,3#N：データの個数、D：入力ノード数、H：隠れ層の数

print('Affineノード')

print('順伝播')
print('X')
x=np.random.randn(N,D)
print(x)
print('W')
w=np.random.randn(D,H)

print(w)
print('b')
b=np.random.randn(H)
print(b)

Affine_Model=Affine(w,b)
Affine_Model_F=Affine_Model.forward(x)

print('Y')
y=Affine_Model_F
print(y)

print('逆伝播')
print('dx')
Affine_Model_B=Affine_Model.backward(Affine_Model_F)
RetuenVal=Affine_Model_B
print(RetuenVal[1])
print('dw')
print(RetuenVal[0])

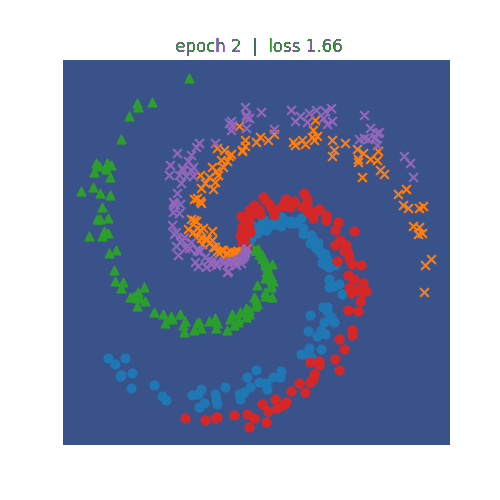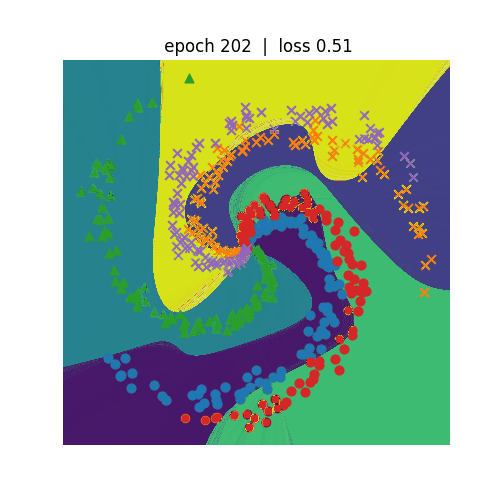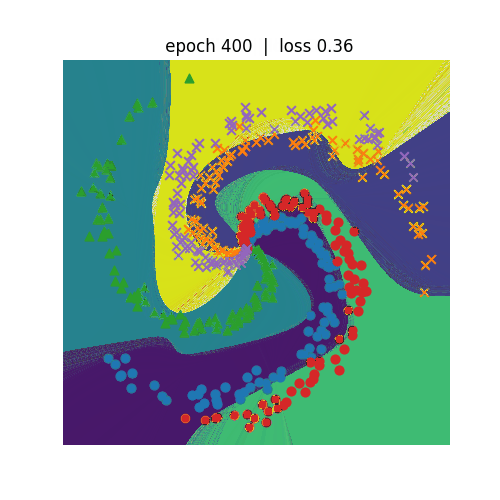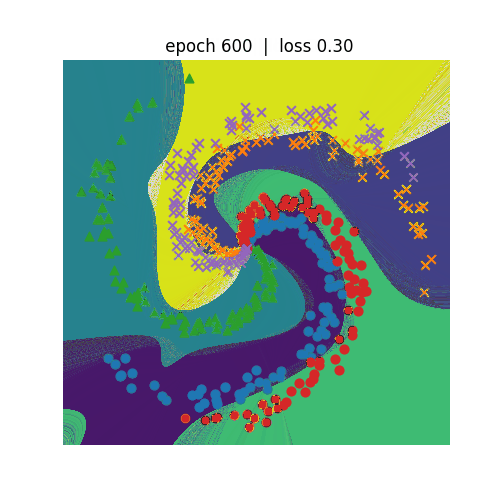
＜Spiralデータセット分類＞

（参考サイト）https://github.com/oreilly-japan/deep-learning-from-scratch-2

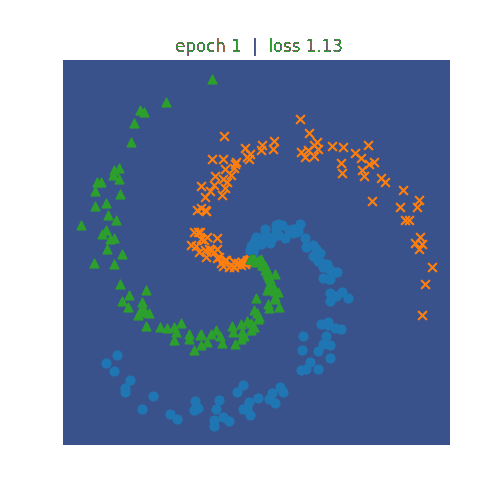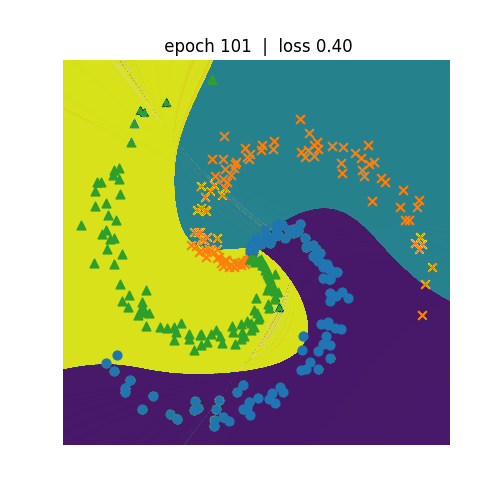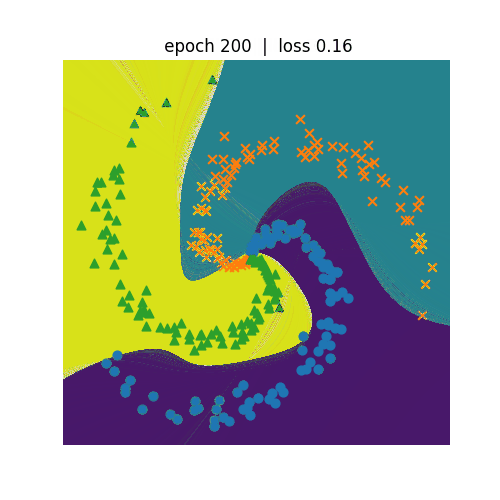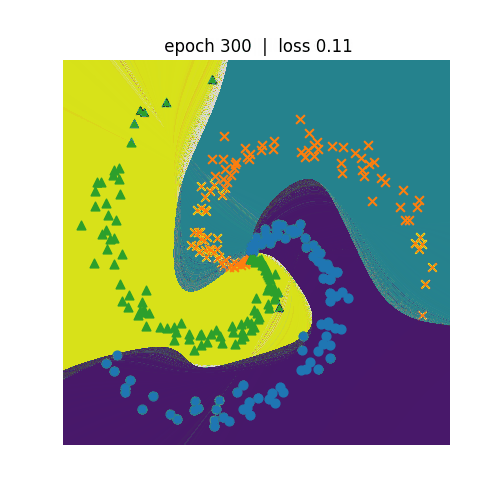
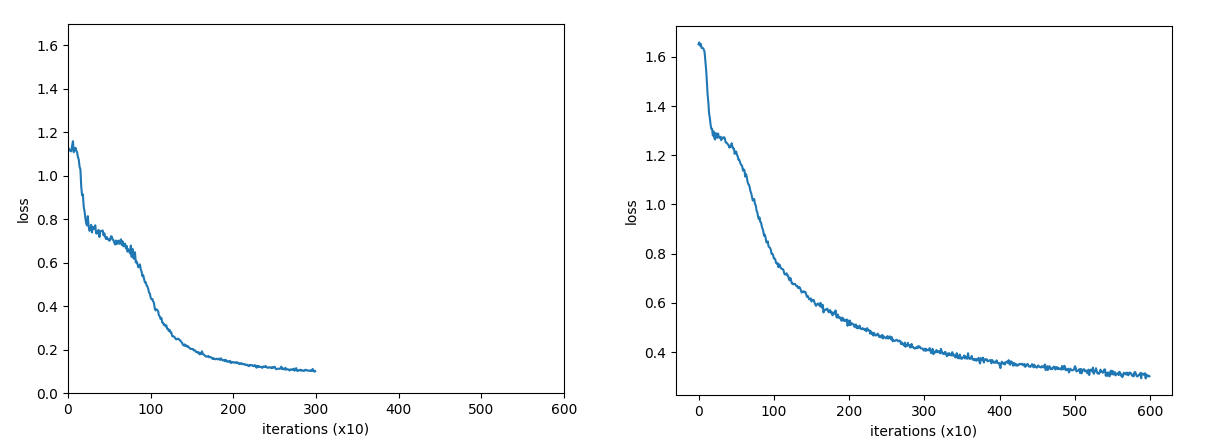
ニューラルネットワークを利用して非線形の分類を行います。左側がＮ＝３、右側がＮ＝５の分類を行うプログラムになります。Ｎ＝５の方が学習のepochが６００まで進めてもloss（誤差）は０．３程度までしか低減しません。Ｎ＝３の方は、epochが３００でも loss（誤差）は０．１まで低減しています。どちらも学習が進むにつれて、種類が違う点を分割しようという意図が伝わってくるような動きになっています。

－－－－－－－－－－－－－

（第２回）ニューラルネットワーク

＜２層 ニューラルネットワーク＞

＜２層 ニューラルネットワーク＋損失関数＞

＜計算グラフ＞

＜ノード①＞

＜ノード②＞

＜ノード③＞

＜Ａｆｆｉｎｅレイヤ＞

＜Spiralデータセット分類＞

機械学習のメモ（その２）

＜２層　ニューラルネットワーク＞

＜２層　ニューラルネットワーク＋損失関数＞