マイコン君　Ｅ資格の勉強メモ（その２）

（第３回）自然言語と分散表現

自然言語処理では単語の意味（正確にはベクトル）を学習して、膨大な文書を集約（その文章の要約）したり、翻訳をしたりします。Ｇｏｏｇｌｅで毎日のように検索して、抽出されたアドレスを見ていますが、これも自然言語処理が利用されています。まずは自然言語処理における単語の原始的な考え方について調べてみます。

＜シソーラス＞

人間が言語の意味をコンピューターに登録する方法です。日々更新される単語（スマホ＝スマートフォン）を随時変更していくのは、かなり大変ですが、単純なプログラムは作成ができそうです。
まずは、シソーラスの代表的なライブラリのＷｏｒｄＮｅｔを使ってみます。そこでＰｙｔｈｏｎのライブラリである、 ntlkをインストールしておきます。
pip install ntlk

以下がＰｙｔｈｏｎのプログラムです。初回のみダウンロードが必要です。（３ＧＢ越えの容量になります・・・＾＾；）

import nltk
from  nltk.corpus import wordnet
#nltk.download('all')#初回

synsets = wordnet.synsets("車",lang='jpn')
for syn in synsets:
    print(syn,":",syn.definition())
car_synset=synsets[0]
synonyms=car_synset.lemma_names("jpn")
print(synonyms)
#['オートモビル', 'オートモービル', 'モーターカー', '乗用車', '四輪車', '自動車', '車']

synsets = wordnet.synsets("犬",lang='jpn')
for syn in synsets:
    print(syn,":",syn.definition())
dog_synset=synsets[0]
synonyms=dog_synset.lemma_names("jpn")
print(synonyms)
#['イヌ', 'ドッグ', '洋犬', '犬', '飼い犬', '飼犬']

車の同類にオートモービルや乗用車、犬の同類にイヌや洋犬などが出力されます。

＜カウントベース＞

コーパスというテキストデータを使って、意味を抽出します。シソーラスのように人力に頼らないため、自動化はできますが、利用するテキストデータと目的が一致していないと利用価値がなくなってしまいます。
そしてコーパスを作成するためには単語の切り取りが必要になります。
以下がＰｙｔｈｏｎのプログラムです。短い英語の文章ですが、単語をＩＤ化して、その文書をＩＤとして表現されています。

# coding: utf-8
import numpy as np


def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
print('コーパス(ID)')
print(Out[0])
print('単語')
print(Out[1])

英語なのでスペースがあれば、単語として抽出が可能ですが、日本語は・・・・＾＾；

＜分散表現＞

シソーラスのように人力に頼らずに単語の意味を理解するために必要な考え方になります。ＭＮＩＳＴでは画像の明るさを学習の入力として利用し、数値が出力（これを正解させる事が目的）していました。単語でも数値として扱うため、分散表現を利用します。
具体的には、単語のベクトルとして表現し、その数値を使って学習させるという方法になります。簡単にできるのは、文章からと周辺の単語の関係性を利用する方法になります。まずは簡単な行列で表現してみます。
以下がＰｙｔｈｏｎのプログラムです。各単語の近い単語を抽出して行列で表現します。

# coding: utf-8
import numpy as np


def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
print('コーパス(ID)')
print(Out[0])
print('単語')
print(Out[1])

vocab_size=len(Out[1])

matrix=create_co_matrix(Out[0],vocab_size,1)
print('共起行列')
print(matrix)

行列で表現ができるようになりました。
下の図が、出力された数値を表にしたもので、各単語に近い（となり）単語が１として表現されています。
これを共起行列といいます。

＜ベクトルの類似度＞

分散表現で単語のベクトルが表現できるようになったので、ベクトルの類似度をコサイン類似度によって表現します。
類似度を算出することができるとどの単語が似ているのか？を数値によって表現ができるようになります。

〇コサイン類似度
２つのｘ．ｙのベクトルがある場合、下の式のとおりになります。 $\large{x=(x_1^2+x_2^2+x_3^2+・・・x_n^2)}$
$\large{y=(y_1^2+y_2^2+y_3^2+・・・y_n^2)}$
$\large{コサイン類似度=\frac{x・y}{||x||・||y||}}$ $\large{=\frac{x_1y_1+x_2y_2+x_3y_3+・・・x_ny_n}{\sqrt{x_1^2+x_2^2+x_3^2+・・・x_n^2　　}・\sqrt{y_1^2+y_2^2+y_3^2+・・・y_n^2　　}}}$

# coding: utf-8
import numpy as np


def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
print('コーパス(ID)')
print(Out[0])
print('単語')
print(Out[1])

vocab_size=len(Out[1])
word_to_id=Out[1]
matrix=create_co_matrix(Out[0],vocab_size,1)
print('共起行列')
print(matrix)

You_matrix=matrix[word_to_id['you']]
I_matrix=matrix[word_to_id['i']]
print('youとＩのベクトル')
print(You_matrix)
print(I_matrix)
print('youとＩのコサイン類似度')
cos_simil=cos_similarity(You_matrix,I_matrix)
print(cos_simil)

実行すると以下の数値が出力されます。
0.7071067691154799
コサイン類似は－１～１なので、近い数値になっています。実際は、sayやand以外はyouに対して同じ数値が出力されます。これは、コーパスが小さすぎるためです。

〇類似度ランキング
類似度が出力できたら、ランキングを計算させます。ランキングを計算することで、さらに単語間の距離が分かり易くなります。自然言語処理のなかでも単語間の関連性を確認するときに順序を見ることが良くあります。
次がプログラムになります。

# coding: utf-8
import numpy as np


def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''類似単語の検索
    :param query: クエリ（テキスト）
    :param word_to_id: 単語から単語IDへのディクショナリ
    :param id_to_word: 単語IDから単語へのディクショナリ
    :param word_matrix: 単語ベクトルをまとめた行列。各行に対応する単語のベクトルが格納されていることを想定する
    :param top: 上位何位まで表示するか
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
word_to_id=Out[1]
id_to_word=Out[2]
print('コーパス(ID)')
print(Out[0])
print('単語')
print(word_to_id)
print(id_to_word)

vocab_size=len(Out[1])

matrix=create_co_matrix(Out[0],vocab_size,1)
print('\n共起行列')
print(matrix)

You_matrix=matrix[word_to_id['you']]
I_matrix=matrix[word_to_id['i']]
print('\nyouとＩのベクトル')
print(You_matrix)
print(I_matrix)
print('\nyouとＩのコサイン類似度')
cos_simil=cos_similarity(You_matrix,I_matrix)
print(cos_simil)

print('\nyouに対するランキング')
most_similar_out=most_similar('you',word_to_id,id_to_word,matrix,top=5)
print(most_similar_out)

実行するとYouに対するランキングが出力されます。
コーパスが小さすぎるため参考になりませんが、ちゃんと出力されています。

＜ＰＰＭＩ（正の相互情報量）＞

ＰＭＩ（相互情報量）は２つの単語が共起した回数を数えて、算出します。

$\large{PMI(x,y)=\log_{2}{\frac{P(x,y)}{P(x)・P(y)}}}$

$p(x)$はコーパス内にｘが何個あるかということで、 $P('car')=\frac{20}{1000}$は1000単語あるコーパス内にcarが20個含まれているという意味です。
$P(x,y)$はコーパス内にｘとyの共起が何個あるかということで、 $p('car','dog')=\frac{10}{1000}$は1000単語あるコーパス内にcarとdogの共起が10個含まれているという意味です。
$C$・・・共起行列
$C(x)$・・・xの出現
$C(y)$・・・ｙの出現
$C(x,y)$・・・xとｙの共起する回数
$N$・・・コーパス単語数（共起行列の合計）

$\large{PMI(x,y)=\log_{2}{\frac{\frac{C(x,y)}{N}}{\frac{C(x)}{N}・\frac{C(y)}{N}}}}$
$\large{PMI(x,y)=\log_{2}{\frac{C(x,y)・N}{C(x)・C(y)}}}$

コーパス内にdogが30個含まれていると
$\large{PMI(car,dog)=\log_{2}{\frac{10・1000}{20・30}}}=4.059$

$\log_{2}$は１より小さいとマイナスになりますが、ＰＰＭＩはＰＭＩのプラス側のみの情報になります。マイナスの時は０にしているので、正のみの情報です。
次がプログラムになります。

# coding: utf-8
import numpy as np


def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''類似単語の検索
    :param query: クエリ（テキスト）
    :param word_to_id: 単語から単語IDへのディクショナリ
    :param id_to_word: 単語IDから単語へのディクショナリ
    :param word_matrix: 単語ベクトルをまとめた行列。各行に対応する単語のベクトルが格納されていることを想定する
    :param top: 上位何位まで表示するか
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
        
def ppmi(C, verbose=False, eps = 1e-8):
    '''PPMI（正の相互情報量）の作成
    :param C: 共起行列
    :param verbose: 進行状況を出力するかどうか
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% done' % (100*cnt/total))
    return M

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
vocab_size=len(Out[1])
matrix=create_co_matrix(Out[0],vocab_size,1)
print('共起行列')
print(matrix)
print('\nPPMI')
print(ppmi(matrix))

実行すると先ほどの共起行列がＰＰＭＩの数値になって出力されています。
[hello］[.]の場合は、
$\large{PMI(’hello’,’．’)=\log_{2}{\frac{1・14　}{2・1　}}}=2.8073$
[say］[goodbye]の場合は、
$\large{PMI(’say’,’goodbye’)=\log_{2}{\frac{1・14　}{4・2　}}}=0.8073$

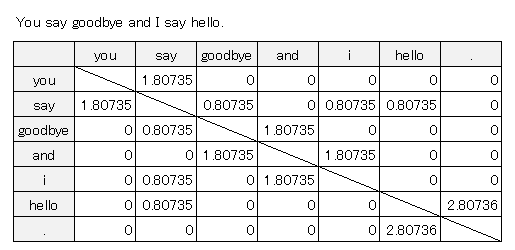
表にすると共起行列で１の部分が数値があります。先ほどはすべて１でしたが、相互情報量を表現することで、数値に変化が生まれています。

＜次元削減＞

特異値分解（ＳＶＤ）をつかって次元削減を行います。
ＰＰＭＩの表をみるとわかりますが、０が多いので、情報量としていらない物があります。そこで、次元削減を行い必要な情報を残しつつ、データを圧縮していきます。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt

def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''類似単語の検索
    :param query: クエリ（テキスト）
    :param word_to_id: 単語から単語IDへのディクショナリ
    :param id_to_word: 単語IDから単語へのディクショナリ
    :param word_matrix: 単語ベクトルをまとめた行列。各行に対応する単語のベクトルが格納されていることを想定する
    :param top: 上位何位まで表示するか
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
        
def ppmi(C, verbose=False, eps = 1e-8):
    '''PPMI（正の相互情報量）の作成
    :param C: 共起行列
    :param verbose: 進行状況を出力するかどうか
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% done' % (100*cnt/total))
    return M

text = 'You say goodbye and I say hello.'
Out=preprocess(text)
word_to_id=Out[1]
id_to_word=Out[2]
vocab_size=len(Out[1])
matrix=create_co_matrix(Out[0],vocab_size, window_size=1)
print('共起行列')
print(matrix)
print('\nPPMI')
print(ppmi(matrix))
MyPPMI=ppmi(matrix)
U,S,V=np.linalg.svd(MyPPMI)
print('\nSVD')
print(U)

for word,word_id in word_to_id.items():
    plt.annotate(word,(U[word_id,0],U[word_id,1]))
plt.scatter(U[:,0],U[:,1],alpha=0.5)
plt.show()

実行すると先ほどの共起行列にＳＶＤが適用されます。この行列の先頭の２次元を抜き出すと２次元に削減されることになります。
２次元にした物をグラフにします。

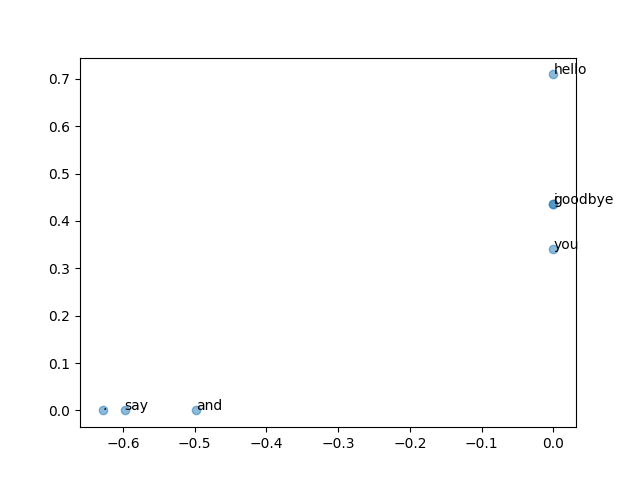
コーパスが小さすぎて意味はないですが、「i,you,hello」「say,and,.」でグループができているように見えます。

＜ＰＴＢデータセット＞

ペン・ツリー・バンク（ＰＴＢ）というデータデータセットを利用して、いままでのプログラムを動作させてみます。
少し時間はかかりますが、入力した単語に近い類似した単語を出力させることができます。

# coding: utf-8
import os
import numpy as np
import matplotlib.pyplot as plt
try:
    import urllib.request
except ImportError:
    raise ImportError('Use Python3!')
import pickle
from sklearn.utils.extmath import randomized_svd
#PTB

url_base = 'https://raw.githubusercontent.com/tomsercu/lstm/master/data/'
key_file = {
    'train':'ptb.train.txt',
    'test':'ptb.test.txt',
    'valid':'ptb.valid.txt'
}
save_file = {
    'train':'ptb.train.npy',
    'test':'ptb.test.npy',
    'valid':'ptb.valid.npy'
}
vocab_file = 'ptb.vocab.pkl'

dataset_dir = os.path.dirname(os.path.abspath(__file__))


def _download(file_name):
    file_path = dataset_dir + '/' + file_name
    if os.path.exists(file_path):
        return

    print('Downloading ' + file_name + ' ... ')

    try:
        urllib.request.urlretrieve(url_base + file_name, file_path)
    except urllib.error.URLError:
        import ssl
        ssl._create_default_https_context = ssl._create_unverified_context
        urllib.request.urlretrieve(url_base + file_name, file_path)

    print('Done')


def load_vocab():
    vocab_path = dataset_dir + '/' + vocab_file

    if os.path.exists(vocab_path):
        with open(vocab_path, 'rb') as f:
            word_to_id, id_to_word = pickle.load(f)
        return word_to_id, id_to_word

    word_to_id = {}
    id_to_word = {}
    data_type = 'train'
    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name

    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()

    for i, word in enumerate(words):
        if word not in word_to_id:
            tmp_id = len(word_to_id)
            word_to_id[word] = tmp_id
            id_to_word[tmp_id] = word

    with open(vocab_path, 'wb') as f:
        pickle.dump((word_to_id, id_to_word), f)

    return word_to_id, id_to_word


def load_data(data_type='train'):
    '''
        :param data_type: データの種類：'train' or 'test' or 'valid (val)'
        :return:
    '''
    if data_type == 'val': data_type = 'valid'
    save_path = dataset_dir + '/' + save_file[data_type]

    word_to_id, id_to_word = load_vocab()

    if os.path.exists(save_path):
        corpus = np.load(save_path)
        return corpus, word_to_id, id_to_word

    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name
    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()
    corpus = np.array([word_to_id[w] for w in words])

    np.save(save_path, corpus)
    return corpus, word_to_id, id_to_word

"""
if __name__ == '__main__':
    for data_type in ('train', 'val', 'test'):
        load_data(data_type)
"""
#PTB
def preprocess(text):
    text = text.lower()#小文字
    text = text.replace('.', ' .')#文字置き換え
    words = text.split(' ')#分割（英語だからスペースで良い）

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''共起行列の作成
    :param corpus: コーパス（単語IDのリスト）
    :param vocab_size:語彙数
    :param window_size:ウィンドウサイズ（ウィンドウサイズが1のときは、単語の左右1単語がコンテキスト）
    :return: 共起行列
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''類似単語の検索
    :param query: クエリ（テキスト）
    :param word_to_id: 単語から単語IDへのディクショナリ
    :param id_to_word: 単語IDから単語へのディクショナリ
    :param word_matrix: 単語ベクトルをまとめた行列。各行に対応する単語のベクトルが格納されていることを想定する
    :param top: 上位何位まで表示するか
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
        
def ppmi(C, verbose=False, eps = 1e-8):
    '''PPMI（正の相互情報量）の作成
    :param C: 共起行列
    :param verbose: 進行状況を出力するかどうか
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% done' % (100*cnt/total))
    return M
#データセット準備（初回ダウンロード）
load_data('train')
load_data('val')
load_data('test')

#データセット読み込み
corpus, word_to_id, id_to_word = load_data('train')
PTB_DataSet = corpus, word_to_id, id_to_word

wordvec_size=100#ランキング表示用行列サイズ

Out=PTB_DataSet

word_to_id=Out[1]
id_to_word=Out[2]
vocab_size=len(Out[1])
matrix=create_co_matrix(Out[0],vocab_size, window_size=2)
print('共起行列')
print(matrix)
print('\nPPMI')
print(ppmi(matrix, verbose=True))
MyPPMI=ppmi(matrix)
#U,S,V=np.linalg.svd(MyPPMI)#stop_low_spec_pc!
U,S,V=randomized_svd(MyPPMI,n_components=wordvec_size,n_iter=5,random_state=None)
print('\nSVD')
print(U.shape)
MySVD_U=U
MySVD_S=V
MySVD_V=S
techacademy = MySVD_U
with open('MySVD_U.pkl', 'wb') as pikle_MySVD_U:
  pickle.dump(techacademy , pikle_MySVD_U)
techacademy = MySVD_S
with open('MySVD_S.pkl', 'wb') as pikle_MySVD_S:
  pickle.dump(techacademy , pikle_MySVD_S)
techacademy = MySVD_V
with open('MySVD_V.pkl', 'wb') as pikle_MySVD_V:
  pickle.dump(techacademy , pikle_MySVD_V)
  
word_vecs=U[:,:wordvec_size]
querys=['you','year','car','toyota']
for query in querys:
    most_similar_out=most_similar(query,word_to_id,id_to_word,word_vecs,top=5)
    print(most_similar_out)

色々な単語を見てみたいのですが、上のプログラムだと毎回十分程度時間がかかるので、時間のかかる出力の、ＰＰＭＩとＳＶＤを経由した出力のＵ、Ｖ、Ｓをpikleファイルとして保存して、１度実行したら、そのファイルから読み出すようにします。
読み出すプログラムは以下のようになります。

import pickle
import os
import numpy as np
url_base = 'https://raw.githubusercontent.com/tomsercu/lstm/master/data/'
key_file = {
    'train':'ptb.train.txt',
    'test':'ptb.test.txt',
    'valid':'ptb.valid.txt'
}
save_file = {
    'train':'ptb.train.npy',
    'test':'ptb.test.npy',
    'valid':'ptb.valid.npy'
}
vocab_file = 'ptb.vocab.pkl'

dataset_dir = os.path.dirname(os.path.abspath(__file__))

def load_vocab():
    vocab_path = dataset_dir + '/' + vocab_file

    if os.path.exists(vocab_path):
        with open(vocab_path, 'rb') as f:
            word_to_id, id_to_word = pickle.load(f)
        return word_to_id, id_to_word

    word_to_id = {}
    id_to_word = {}
    data_type = 'train'
    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name

    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()

    for i, word in enumerate(words):
        if word not in word_to_id:
            tmp_id = len(word_to_id)
            word_to_id[word] = tmp_id
            id_to_word[tmp_id] = word

    with open(vocab_path, 'wb') as f:
        pickle.dump((word_to_id, id_to_word), f)

    return word_to_id, id_to_word

def load_data(data_type='train'):
    '''
        :param data_type: データの種類：'train' or 'test' or 'valid (val)'
        :return:
    '''
    if data_type == 'val': data_type = 'valid'
    save_path = dataset_dir + '/' + save_file[data_type]

    word_to_id, id_to_word = load_vocab()

    if os.path.exists(save_path):
        corpus = np.load(save_path)
        return corpus, word_to_id, id_to_word

    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name
    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()
    corpus = np.array([word_to_id[w] for w in words])

    np.save(save_path, corpus)
    return corpus, word_to_id, id_to_word

def cos_similarity(x, y, eps=1e-8):
    '''コサイン類似度の算出
    :param x: ベクトル
    :param y: ベクトル
    :param eps: ”0割り”防止のための微小値
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''類似単語の検索
    :param query: クエリ（テキスト）
    :param word_to_id: 単語から単語IDへのディクショナリ
    :param id_to_word: 単語IDから単語へのディクショナリ
    :param word_matrix: 単語ベクトルをまとめた行列。各行に対応する単語のベクトルが格納されていることを想定する
    :param top: 上位何位まで表示するか
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return

#データセット読み込み
corpus, word_to_id, id_to_word = load_data('train')
PTB_DataSet = corpus, word_to_id, id_to_word

wordvec_size=100#ランキング表示用行列サイズ

Out=PTB_DataSet

word_to_id=Out[1]
id_to_word=Out[2]

#モデルを読みだす
with open('MySVD_U.pkl', 'rb') as  pikle_MySVD_U:
  MySVD_U = pickle.load( pikle_MySVD_U)

wordvec_size=100
word_vecs=MySVD_U[:,:wordvec_size]
querys=['you','year','car','toyota','dog','disney']
for query in querys:
    most_similar_out=most_similar(query,word_to_id,id_to_word,word_vecs,top=5)
    print(most_similar_out)

上のプログラムの
querys=['you','year','car','toyota','dog','disney']
の単語を変更すると記載した単語の近い単語が出力されます。以下が出力したデータです。

[query] you
 i: 0.6437749862670898
 we: 0.6247314810752869
 someone: 0.5839582085609436
 anybody: 0.5741029381752014
 else: 0.5290864706039429
None
[query] year
 quarter: 0.6446389555931091
 month: 0.6302509903907776
 next: 0.6293458938598633
 earlier: 0.6064082980155945
 last: 0.595670759677887
None
[query] car
 auto: 0.5804438591003418
 cars: 0.5393903851509094
 luxury: 0.5386356711387634
 corsica: 0.5255438089370728
 truck: 0.5238440632820129
None
[query] toyota
 motor: 0.7535560131072998
 motors: 0.6614410877227783
 nissan: 0.6533970236778259
 honda: 0.6042033433914185
 lexus: 0.5965747833251953
None
[query] dog
 incorporated: 0.6439036130905151
 corner: 0.5795753002166748
 signature: 0.5559136867523193
 naczelnik: 0.5411404371261597
 elegant: 0.5393158793449402
None
[query] disney
 merck: 0.6706962585449219
 warner-lambert: 0.6388406157493591
 eastman: 0.6197047829627991
 walt: 0.6129381060600281
 lilly: 0.6063474416732788
None

今回は自然言語処理についてしらべてみました。実用性は全くないですが、どのようにして単語を数値化するか？など興味深い内容だったです。ＰＴＢのデータセットも英語ですが、類似している単語がちゃんと表示されています。データファイルに「ptb.test.txt」がありますが、内容をみるとＮＥＷＳの記事のような物が保存されており、TOYOTAの近いものにNISSANや HONDAなど「なるほど」と思うような単語が出力されていて、感心しました。

－－－－－－－－－－－－－