(第1回)行列について
機械学習では行列が多く使われています。PythonではNumpyというライブラリが優秀で、意識して考えなくても 簡単に行列の計算ができますが、E資格では「線形代数」として、ベクトルや行列の理解をすることが必要です。
勉強がてらまずは行列について調べてみようと思います。
ベクトルについて
まずはベクトルから、ベクトルは下のように表します。左側が縦ベクトル(7次元)。右側がその転置となります(横ベクトル)。

次は、xがサイコロを1個、yがサイコロを2個、振った時の出た目の合計のデータです。xは転置で表していますが、 どちらも同じ意味です。またxとyの足し算、引き算は単純に、各数値を計算するだけですが、
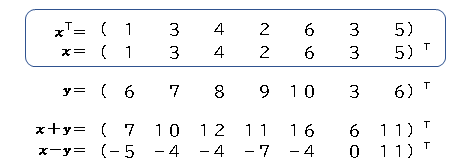
掛け算の時は、x(横ベクトル)とy(縦ベクトル)を計算すると内積となり、スカラーが出力されます。
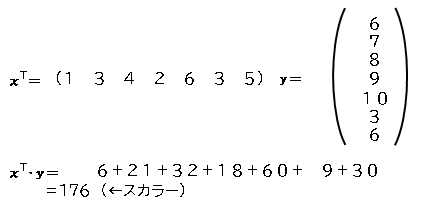
しかし、x(縦ベクトル)とy(横ベクトル)の掛け算は全く異なった結果となり、行列が出力されます。

<Pytthonによる計算>
ベクトルの計算を実際にPythonで行います
結果
Pythonで計算する場合は、転置を行うため。2次元の配列になっていますが、ちゃんと計算できています。
行列について
縦と横のベクトルの掛け算が行列になりますが、n行m列の配列を持っているもので、機械学習のデータ処理には欠かせません。 ここでは行列について調べてみます。
いきなりですが、連立方程式を行列を使って、解を求めます。

これは行列の基本変形で、xとyの部分を1にするように変形させることで、連立方程式の解を求めることができます。 x、y、zの3つの物でも同じように変形することで、解を求めることができます。
<対称行列>
対称行列とは、自身の転換行列と一致する、正方行列の事。
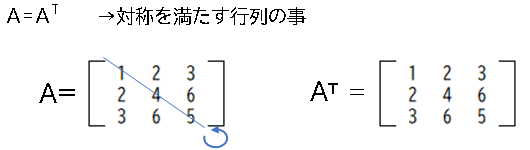
<転置行列>
転置行列とは、m 行 n 列の行列 A に対して A の (i, j) 要素と (j, i) 要素を入れ替えてできる
n 行 m 列の行列の事。斜線に対して対称に入れ替えるイメージ。
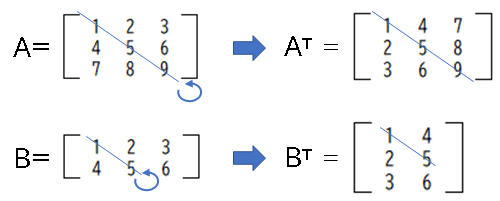
<逆行列>
行列Aの逆行列はA-1。⇒A×A-1=Eで表す。
また、n行n列のA、Bの正方行列は、n×nの単位行列Eにおいて
AB=BA=E を満たす
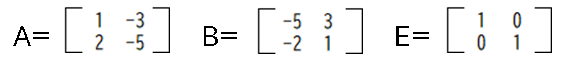
そしてAの逆行列Bを求める時は、AとEを以下の様に簡約化する。
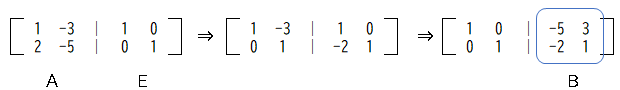
<直交行列>
直交行列とは、転置行列と逆行列が等しくなる正方行列の事。
ATA=AAT=E を満たす 正方行列の事。
-------------
