マイコン君　Ｅ資格の勉強メモ

（第７回）誤差逆伝播法

前回のＭＮＩＳＴの学習で、せっかく作った順伝播法を使っていませんでした。実行してみるとわかりますが、遅くて使えません。微分による勾配の計算をすると、すべてのパラメーターで同じような計算を繰り返して行うため、非常に時間がかかります。第６回のプログラムの順伝播、誤差逆伝播法を入れ替えて実行すると良くわかります。

＜簡単な逆伝播法＞

まずは簡単な順伝播法と逆伝播法を確認します。順伝播はＡ～Ｄがきまれば、Ｚは容易に決まります。
逆伝播の場合は、連鎖律を考えると、∂z/∂zからＡの方向へ戻る場合、約分され最終的には、∂ｚ／∂ａとなります。
∂ｚが１の場合（Ｚが１増える場合）、∂ａ＝１／９となります。微分をしてみるとわかるのですが、逆伝播での乗算は、∂z/∂ｘ＝ＹのようにＸ側にＹが、加算は、∂ｘ/∂ａ＝１のように、何も変化しないという部分が特徴的です。乗算は逆転して流れ、加算はそのまま流すという形です。

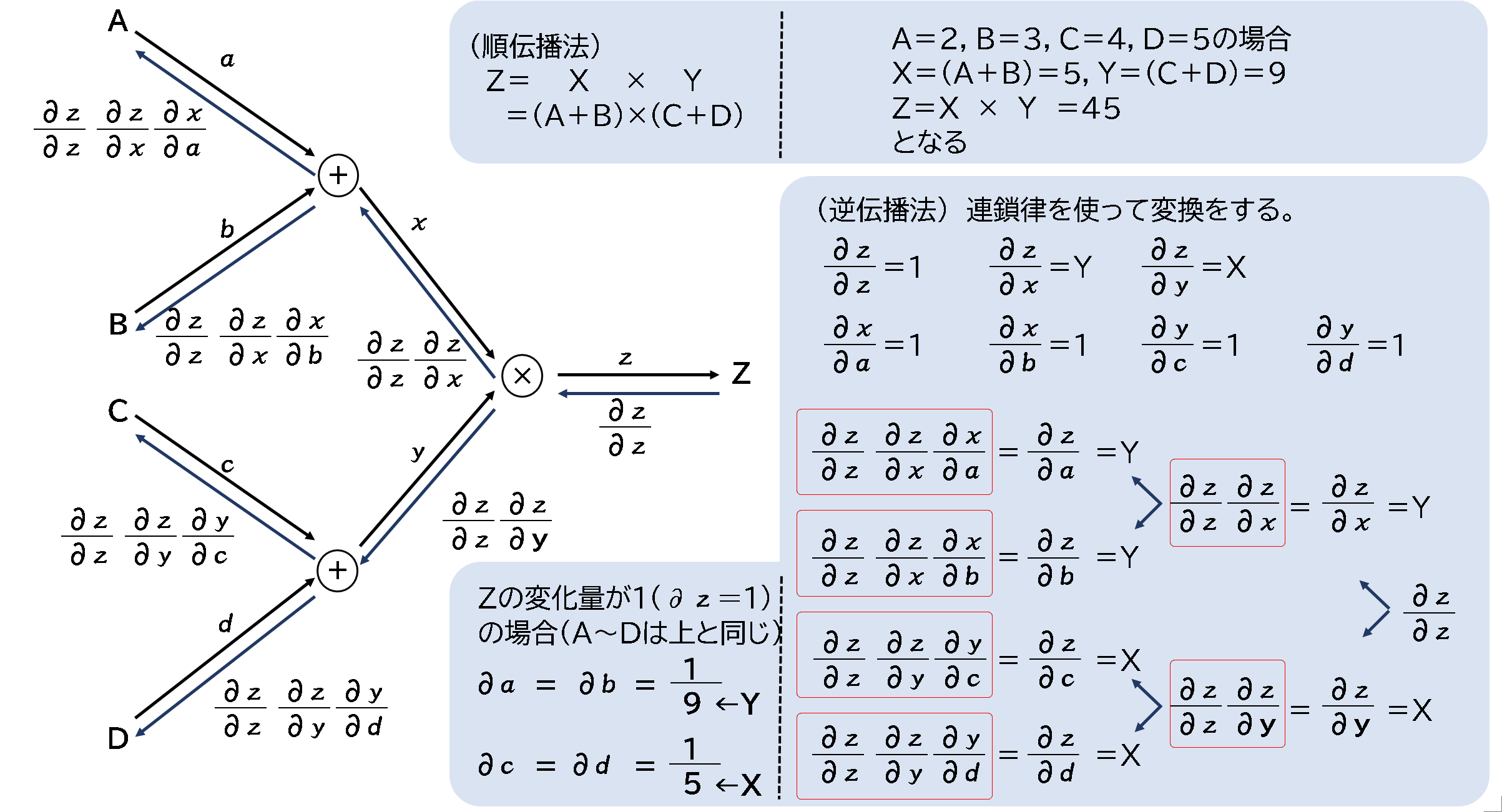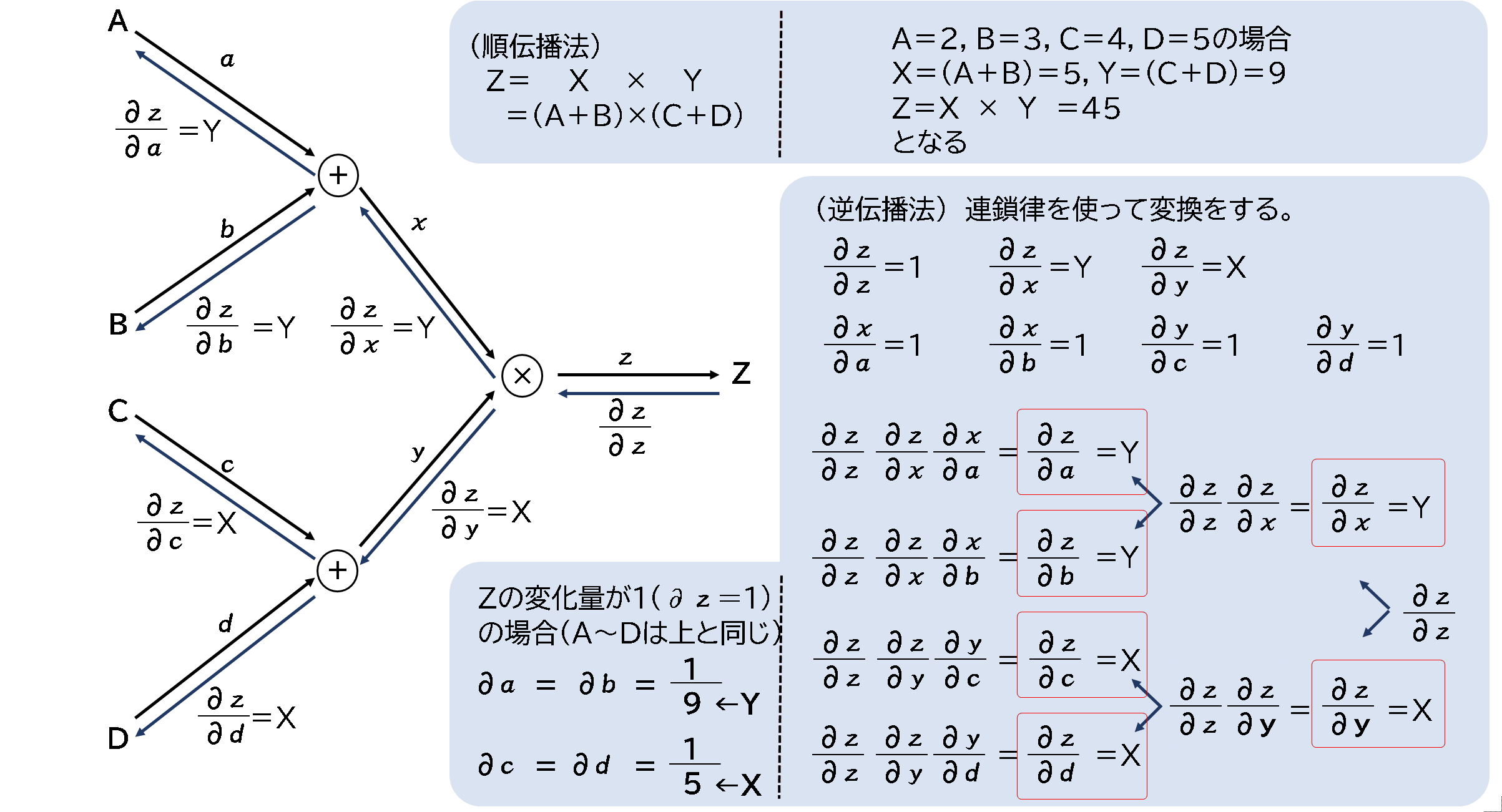
一見「逆伝播の方が複雑」と感じるかもしれません。しかし、順伝播はＺを計算するためにＡ～Ｄをすべて計算する必要があります。逆伝播はＺから計算するため、Ａ～Ｄを同時に算出できるため、計算回数が少なくすることが可能です。

Ｐｙｔｈｏｎで実行すると以下のようになります。

import numpy as np
#---乗算レイヤの実装

class MulLayer:
    def __init__(self):
        pass
    def forward(self,x,y):
        self.x=x
        self.y=y
        out=x*y
        return out
    def backward(self,dout):
        dx=dout*self.y
        dy=dout*self.x
        return dx,dy


#---加算レイヤの実装

class ADDLayer:
    def __init__(self):
        pass
    def forward(self,x,y):
        self.x=x
        self.y=y
        out=x+y
        return out
    def backward(self,dout):
        dx=dout*1
        dy=dout*1
        return dx,dy
    
#---乗算と加算レイヤ組み合わせ実装    
print('---乗算と加算レイヤ組み合わせ実装')


A=2.
B=3.
C=4.
D=5.
#X=A+B,Y=C+D,Z=X*Yの組み合わせ
print('順伝播：Ａ～Ｄ→Ｚ')
X_Layer=ADDLayer()
Y_Layer=ADDLayer()
Z_Laer=MulLayer()
Z_F_OUT=Z_Laer.forward(X_Layer.forward(A,B),Y_Layer.forward(C,D))
print(Z_F_OUT)#45.0

print('逆伝播：ｄｚ＝１→ｄａ～ｄｄ')
print('ｄｚ／ｄｘ，ｄｚ／ｄｙ')
Z_B_OUT=Z_Laer.backward(1.)
print(Z_B_OUT)#(9.0, 5.0)
print('ｄｚ／ｄａ，ｄｚ／ｄｂ')
X_B_OUT=X_Layer.backward(Z_B_OUT[0])
print(X_B_OUT)#(9.0, 9.0)
print('ｄｚ／ｄｃ，ｄｚ／ｄｄ')
Y_B_OUT=Y_Layer.backward(Z_B_OUT[1])
print(Y_B_OUT)#(5.0, 5.0)

乗算レイヤの「MulLayer」と加算レイヤの「ADDLayer」クラスを作成し、それぞれに順伝播（forward）、逆伝播（backward）関数を作成します。Ａ～Ｄの数値を使って、順伝播を計算し、Ｚから逆方向にＸ，Ｙを計算、Ａ～Ｄを計算することで、∂ｚ＝１（Ｚが１変化）した時に、∂ｚ／∂ａ＝∂ｚ／∂ｂ＝９、∂ｚ／∂ｃ＝∂ｚ／∂ｄ＝５となり、結果的には∂ａ＝∂ｂ＝１／９、∂ｃ＝∂ｄ＝１／５となります。これは、手で計算したときと同じ結果になっています。
今回の例は、４つの入力から２個の隠れ層を経由して、１個の出力でしたので、どっちから計算しても同じ計算量に感じるかもしれませんが、実際の機械学習は多くの入力層（ＭＮＩＳＴは７８４個）になりますので、はっきりとした差が感じられます。

＜ＲｅＬＵ＞

ＲｅＬＵ関数を誤差逆伝播法に対応できるようにします。加算、乗算については、上記で確認したとおり、逆伝播では加算はそのまま、乗算は逆の出力になるという事が確認できました。ＲｅＬＵは０以外は、そのまま流すということなので、逆伝播でも同じになります。
forward：[[2.,0.1],[2.,-0.2]]
backward：[[-2.,-0.1],[-2.,-0.2]]
逆伝播結果：[[-2. -0.1] [-2. 0. ]]　←順伝播で－０．２の部分だけが「０」となる。
順伝播で入力した時に「マイナス」がある場合は、逆伝播の時「０」になります。そのため、結果は、上記のように順伝播でマイナス以外が算出されています。スイッチのような機能になっています。

import numpy as np
print('---ReLUレイヤの実装')
class ReLU_Layer:
    def __init__(self):
        self.mask=None
    def forward(self,x):
        self.mask=(x<=0)
        out=x.copy()
        out[self.mask]=0
        return out

    def backward(self,dout):
        dout[self.mask]=0
        dx=dout
        
        return dx
test_Relu=ReLU_Layer()
test_Relu_F=test_Relu.forward(np.array([[2.,0.1],[2.,-0.2]]))
test_Relu_B=test_Relu.backward(np.array([[-2.,-0.1],[-2.,-0.2]]))

print(test_Relu.mask)
print(test_Relu_F)
print(test_Relu_B)

＜Ｓｉｇｍｏｉｄ＞

Ｓｉｇｍｏｉｄ関数を誤差逆伝播法に対応できるようにします。第２回で調べた式は

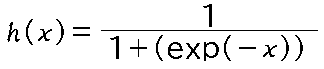
これを分解して微分していきます。

まずはシグモイド関数をｒとｔに置き換えます。
$\large{h(x)=\frac{1}{1+exp(-x)}}$
$\large{r=1+exp(-x)}$
$\large{t=\frac{1}{1+exp(-x)}=\frac{1}{r}=r^{-1}}$
次にそれぞれを微分します。
$\large{h(x)^{'}=\frac{∂t}{∂x}=\frac{∂t}{∂r}\cdot\frac{∂r}{∂x}}$
$\large{\frac{∂t}{∂r}=-ｒ^{-2}}$
$\large{\frac{∂r}{∂x}=-exp(-x)}$
$h(x)^{'}$の式を展開して
$\large{h(x)^{'}=\frac{exp(-x)}{r^{2}}=\frac{exp(-x)}{(1+exp(-x))^{2}}=\frac{exp(-x)}{(1+exp(-x))^{2}}＋\frac{1}{(1+exp(-x))^{2}}－\frac{1}{(1+exp(-x))^{2}}}$
$\large{=\frac{1}{(1+exp(-x))}\cdot(\frac{1+exp(-x)}{(1+exp(-x))}-\frac{1}{(1+exp(-x))})}$
$\large{=t\cdot(1-t)}$
となります。
Ｐｙｔｈｏｎでプログラムを作成すると以下のとおりになります。順伝播で求めたＯＵＴ（ｔ）をそのまま使って、（１－ｔ）・ｔで逆伝播が求められています。

import numpy as np
import matplotlib.pyplot as plt
print('---Sigmoidレイヤの実装')
class Sigmoid_Layer:
    def __init__(self):
        self.out=None
    def forward(self,x):
        out=1/(1+np.exp(-x))
        self.out=out
        return out

    def backward(self,dout):
        dx=dout*(1.0-self.out)*self.out
        
        return dx
test_Sigmoid=Sigmoid_Layer()
test_Sigmoid_F=test_Sigmoid.forward(np.array([[100.,0.1],[2.,-0.2]]))
test_Sigmoid_B=test_Sigmoid.backward(np.array([[-2.,-0.1],[-2.,-0.2]]))

print(test_Sigmoid.out)
print(test_Sigmoid_F)
print(test_Sigmoid_B)

Graph_X=np.arange(-10,10,.1)

test_Sigmoid2=Sigmoid_Layer()
test_Sigmoid_F=test_Sigmoid2.forward(Graph_X)
test_Sigmoid_B=test_Sigmoid2.backward(test_Sigmoid_F)

plt.plot(Graph_X,test_Sigmoid_F,label="forward")
plt.plot(Graph_X,test_Sigmoid_B,label="backward")
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()

グラフも出力すると、次のとおりになっています。

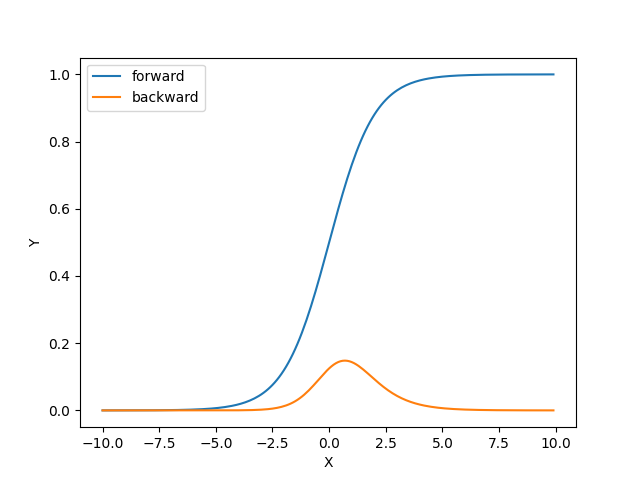
シグモイドの順伝播を微分したグラフになってます。

＜Affine＞

活性化関数では、１層の計算でしたが、実際は多層で処理をする必要があります。

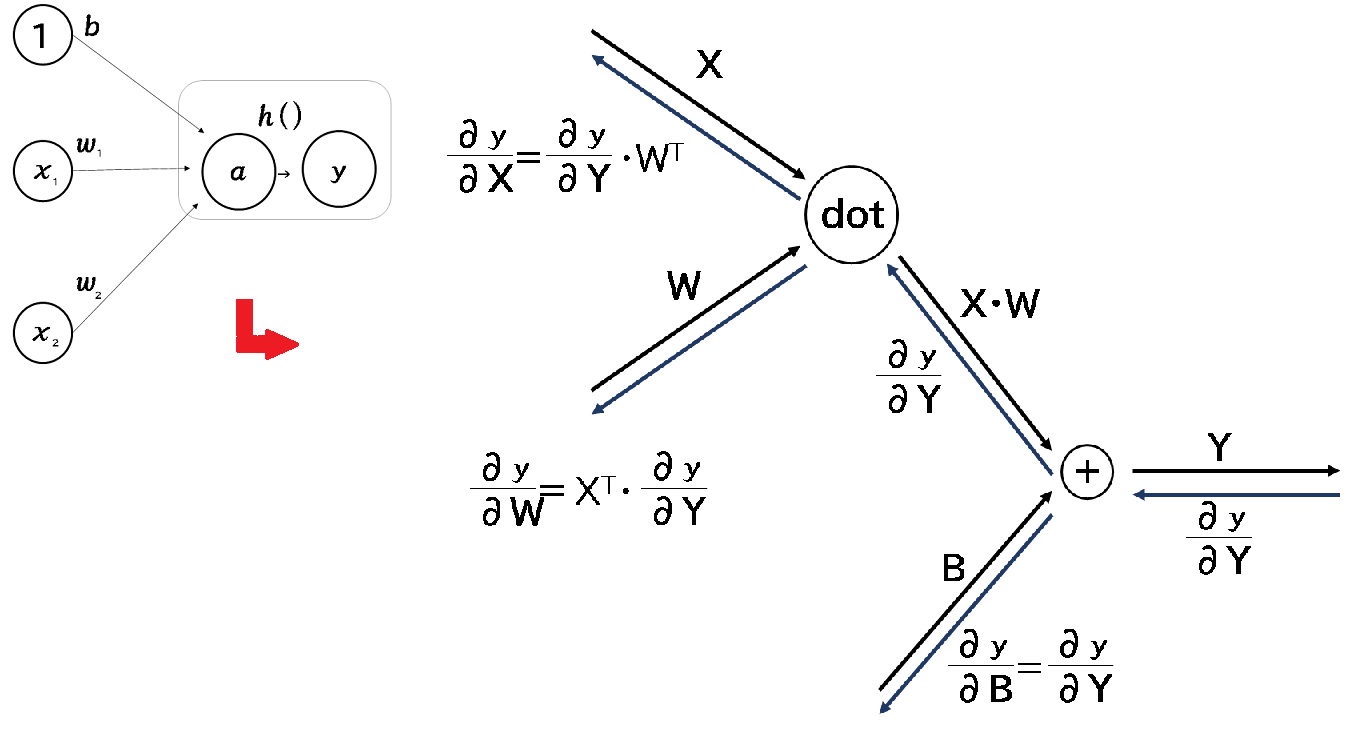
$\large{a=b+w_{1}x_{1}+w_{2}x_{2}}$ 　$\large{y=h(a)}$

↓

$\large{\frac{∂y}{∂X}=\frac{∂y}{∂Y}\cdot W^{T}}$　　　 $\large{\frac{∂y}{∂W}=X^{T}\cdot \frac{∂y}{∂Y}}$　　　 $\large{\frac{∂y}{∂B}=\frac{∂y}{∂Y}}$

上記のように、単層→多層で処理するために、Ａｆｆｉｎｅ変換を行い、逆伝播法を計算します。逆伝播は微分で求めるのですが、変換が大変なので、暗記することにします。

PythonでＡｆｆｉｎｅ変換を実行します。
まずは、第６回のメインプログラムを以下の物にします。ほとんど同じですが、最後に「import pickle」が追加されています。これは、重みづけのデータをファイルに書き出すライブラリです。（便利）この重みづけのファイルを使えば、学習済みのモデルとして利用ができます。この重みづけのＷ１，ｂ１を利用するために学習をして、ファイルを書き出します。

print('---mnist')
# coding: utf-8
import sys, os
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist
from two_layer_net import TwoLayerNet

# データの読み込み
#---mnist---
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
#---dummmy---
#x_train=np.random.rand(60000,784)#ダミー入力
#t_train=np.random.rand(60000,10)#ダミー入力
#x_test=np.random.rand(10000,784)#ダミー入力
#t_test=np.random.rand(10000,10)#ダミー入力
#-------

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000  # 繰り返しの回数を適宜設定する
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 勾配の計算
    #grad = network.numerical_gradient(x_batch, t_batch)#順伝播（遅くて使えない）
    grad = network.gradient(x_batch, t_batch)#誤差逆伝播法
    
    # パラメータの更新
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

# グラフの描画
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()


import pickle
techacademy = network.params['W1']
with open('My_w1.pkl', 'wb') as pikle_w1:
  pickle.dump(techacademy , pikle_w1)
  
techacademy = network.params['W2']
with open('My_w2.pkl', 'wb') as pikle_w2:
  pickle.dump(techacademy , pikle_w2)
  
techacademy = network.params['b1']
with open('My_b1.pkl', 'wb') as pikle_b1:
  pickle.dump(techacademy , pikle_b1)
  
techacademy = network.params['b2']
with open('My_b2.pkl', 'wb') as pikle_b2:
  pickle.dump(techacademy , pikle_b2)

「My_w1.pkl」「My_b1.pkl」の２個のファイルを使って、以下のプログラムを実行します。ペイントブラシで、５６ｘ５６ピクセルの画像を作り、同じフォルダに「test.png」と保存します。
実行すると自分の作成した画像が１度表示され、もう一度別の画像が表示されます。これは、「test.png」を順伝播して、出力されたデータを逆伝播して、入力のデータを算出した結果です。

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import pickle

print('---Affineレイヤの実装')

class Affine_Layer:
    def __init__(self,W,b):
        self.W=W
        self.b=b
        self.x=None
        self.dw=None
        self.db=None
        
    def forward(self,x):
        self.x=x
        out=np.dot(x,self.W)+self.b
        return out
    def backward(self,dout):
        dx=np.dot(dout,self.W.T)
        self.dw=np.dot(self.x.T,dout)
        self.db=np.sum(dout,axis=0)
        return dx

#モデルを読みだす
with open('My_w1.pkl', 'rb') as  pikle_w1:
  My_w1 = pickle.load( pikle_w1)
with open('My_b1.pkl', 'rb') as  pikle_b1:
  My_b1 = pickle.load( pikle_b1)
print(My_w1.shape)
print(My_b1.shape)

#自分で書いた文字を表示
myimg = Image.open('test.png').convert('L')
myimg.thumbnail((28, 28)) # 28*28に変換
myimg = np.array(myimg) # numpy arrayに変換
plt.imshow(myimg)
plt.show()

#自分で書いた文字
myimg_array=np.array(myimg.flatten())
test_Affine2=Affine_Layer(My_w1,My_b1)
MyMojiPic=myimg_array.reshape(784, 1)
MyMojiPic=MyMojiPic/255

# 順伝播を計算
Y = test_Affine2.forward(MyMojiPic.T)
print('Y')
print(Y.shape)
print(Y)

# 逆伝播を計算
dX = test_Affine2.backward(Y)
print('dx')
print(dX.shape)
print(dX)

# 逆伝播で出力された画像を表示
myimg = dX.reshape(28,28) # numpy arrayに変換
plt.imshow(myimg)
plt.show()

真っ黒の５６Ｘ５６を順伝播させたり、ランダムのダミーを学習したモデルで、順伝播→逆伝播したしてみると面白いかもしれません。100000回学習したモデル（ｗ１，ｂ１）とランダムのモデルでは、はっきりと違いが出ています。(以下）

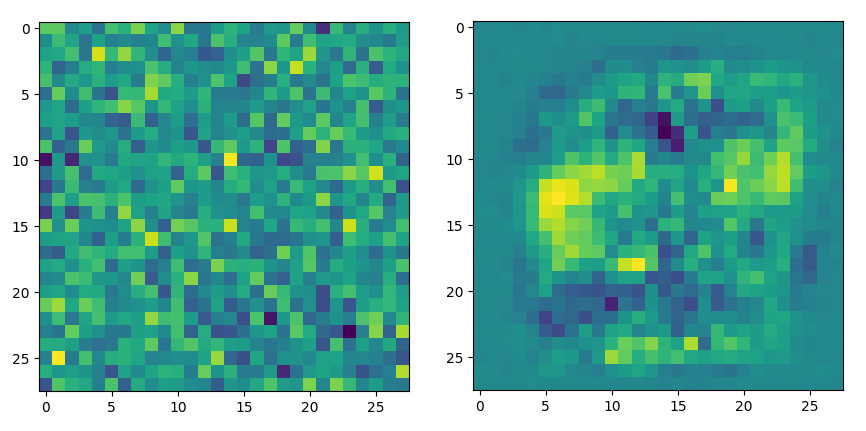
左がランダムのモデル。右が100000回学習したモデルで、９７％程度の正解率です。学習したモデルは、文字を書く部分を重みづけしているような画像になっています。ランダムデータのモデルは、ランダム感がでていて、おもしろいです。

＜Softmax－ｗith－Loss＞

出力層のソフトマックスの逆伝播法についてです。

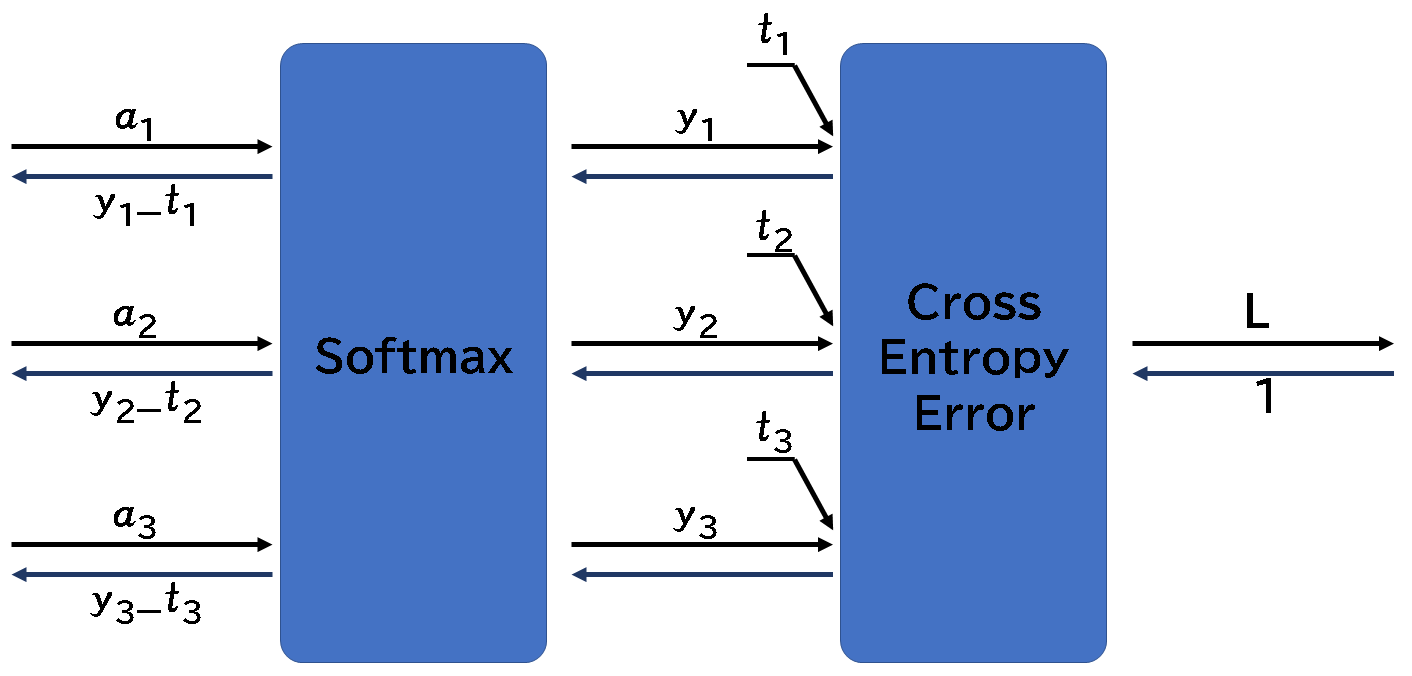
非常に単純なので驚きますが、$(y_{1}-t_{1},y_{2}-t_{2},y_{3}-t_{3})$になっています。
Ｐｙｔｈｏｎで実行してみるとわかりますが、逆伝播では、Ｓｏｆｔｍａｘの出力から、教師データを引き算した結果が得られます。

import numpy as np

print('---Softmax－ｗith－Lossレイヤの実装')


def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)   # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if t.size == y.size:
        t = t.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
 

class SoftmaxWithLoss:
    def __init__(self):
        self.loss=None#損失
        self.x=None#sofmaxの出力
        self.y=None#教師データ
        
    def forward(self,x,t):
        self.t=t
        self.y=softmax(x)
        self.loss=cross_entropy_error(self.y,self.t)
        
        return self.loss
    def backward(self,dout=1):
        batch_size=self.t.shape[0]
        dx=(self.y-self.t)/batch_size
        return dx
#正解が２
t=np.array([[0,0,1,0,0,0,0,0,0,0]])

#計算結果が２が確率が高い
x=np.array([[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]])

test_SoftmaxWithLoss=SoftmaxWithLoss()
print(test_SoftmaxWithLoss)
loss = test_SoftmaxWithLoss.forward(x,t)
print(test_SoftmaxWithLoss.t)
print(test_SoftmaxWithLoss.y)
print(loss)
dx = test_SoftmaxWithLoss.backward()
print(dx)

出力を比較すると
Softmax：[0.098,0.093,0.162,0.088,0.093,0.098,0.088,0.098,0.088,0.088]
逆伝播：[0.098,0.093,-0.837,0.088,0.093,0.098,0.088,0.098,0.088,0.088]
のように教師データが正解の部分がマイナスされていることがわかります。