（第１１回）過学習

訓練データにばかり適用しすぎて、そのほかのデータにはうまく対応できない（＝汎化性能が低い）学習を過学習と言います。

＜ノルムについて＞

過学習にならないように、重みの減衰をさせる（罰則を設ける）方法がありますが、ノルムについて理解しておく必要があります。 Ｌ１ノルムの正則化（Ｌａｓｓｏ回帰）、Ｌ２ノルムの正則化（Ｒｉｄｇｅ回帰）などが機械学習を勉強するとよく出てくる言葉です。
〇Ｌ１ノルム
絶対値の和になります。
$||x_{1}||=|w_{1}|+|w_{2}|+|w_{3}|+・・・|w_{n}|$
〇Ｌ２ノルム
２乗の和になります。
$||x_{2}||=\sqrt{|w_{1}|^{2}+|w_{1}|^{2}+|w_{1}|^{2}+・・・|w_{n}|^{2}}$
下のプログラムを実行します。

まずは基準０，０→４，３の矢印が表示されます。（４，３）の場合Ｌ０ノルムは０以外の数値が２個あるので、「２」となり、Ｌ１は「７」、Ｌ２は「５」です。 ノルムの数が大きくなると徐々に四角形になります。

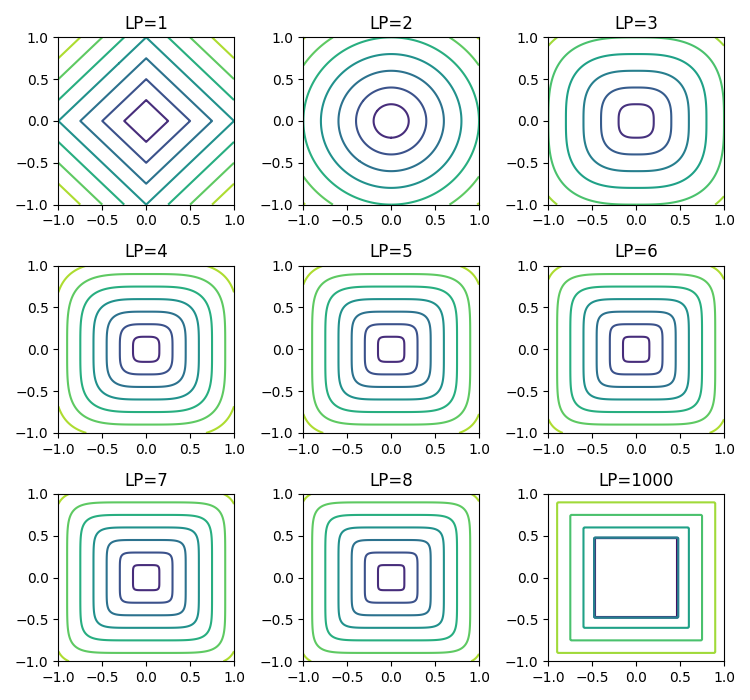
ＸとＹがノルムの数値によって、計算された高さを等高線で表示しています。
$\large{||Ｚ_{p}||=\sqrt[p]{（|ｘ|^{p}+|y|^{p}}}$
ｐ＝１（Ｌ１）、ｐ＝２（Ｌ２）で、ｐ＝∞（Ｌ∞）も利用される事があるようです。 通常はＬ２ノルムが良く利用されるので、この形で正則化を行い重みを減衰させることで、過学習を発生させないようにしています。

＜Ｗｅｉｇｈｔ　Ｄｅｃａｙ＞

損失関数に罰則を加える手法です。Ｌ２ノルムをペナルティとして利用します。

$\LARGE{\frac{1}{2}λW^{2}}$
λは正則化の強さをコントロールするハイパーパラメータ
1/2はW^2を微分した結果をλWにするための調整用の定数

この項を損失関数に加えて重みが大きく変更されないようにしています。 下のプログラムを実行します。（第１０回と同じディレクトリに保存して実行します）

multi_layer_net.pyの 「weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)」
が損失関数に加算している部分になります。

訓練データとテストデータの精度をweight_decay_lambdaの数値が０（なし）と０．１で比較すると、訓練データが１００％に 到達しなくなっています。テストデータの正解率はどちらも変わりません。訓練データとテストデータの正解率の差が小さくなっており、 過学習が抑制できていることがわかります。

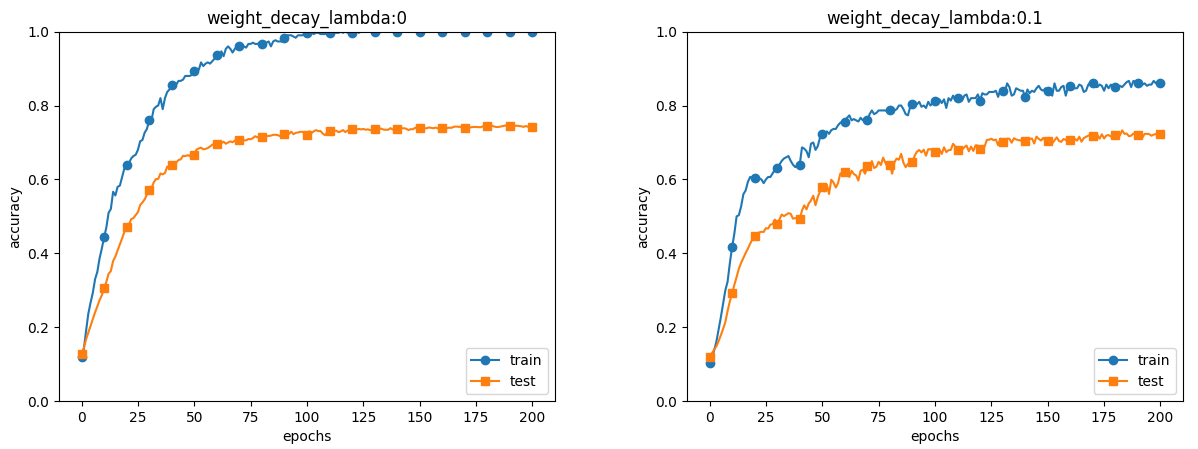
＜Dropout＞

ニューラルネットワークのニューロンをランダムで選択して、その経路を遮断してしまう方法です。
入力と同じ形状の配列をランダムで形成し、その数値が、doropout_ratioより大きいもニューロンのみを使用します。（ratio以下の物は遮断） 下のプログラムを実行します。（第１０回と同じディレクトリに保存して実行します）

訓練データとテストデータの精度をＤｏｒｏｐｏｕｔの有無で比較すると、訓練データが１００％に 到達しなくなっています。dropout_ratio＝０．２で行っていますが、訓練データとテストデータの正解率の差が小さくなっており、 過学習が抑制できていることがわかります。

－－－－－－－－－－－－－