マイコン君　Ｅ資格の勉強メモ

（第４回）損失関数

ニューラルネットワークで入力から出力を得ることができるようになりましたが、ほしい出力が得られる、重み（ｗ）、バイアス（ｂ）を決める必要があります。しかし、考え無しに計算をしても、良い結果は得られません。その目標にする数値が損失関数となります。損失関数を小さくすることこそが、目標になります。
損失関数の「２乗和誤差」「交差エントロピー誤差」について調べます。

＜２乗和誤差＞

ニューラルネットワークで出力（ソフトマックス）された数値と正解の数値の差異を誤差として算出します。ここで正解の数値という物が「教師データ」となります。
具体的には、

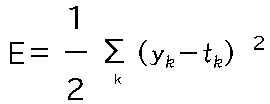
のように、（ニューラルネットワークの出力と正解の差の２乗の総和）／２となります。
またPythonで計算すると以下のようになります。正解が２の場合で、出力も２の場合は、０．１程度の誤差ですが、出力が７になると０．６程度の誤差になります。

import numpy as np
print('---２乗和誤差')

def sum_squared_error(y,t):
    return 0.5*np.sum((y-t)**2)

#正解が２
t=[0,0,1,0,0,0,0,0,0,0]
#計算結果が２が確率が高い
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
#２乗和誤差
z=sum_squared_error(np.array(y),np.array(t))
print(z)#0.0975

#計算結果が７が確率が高い
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
#２乗和誤差
z=sum_squared_error(np.array(y),np.array(t))
print(z)#0.5975

＜交差エントロピー誤差＞

2乗和誤差は、正解ラベル以外の出力（ソフトマックス）も影響を受けますが、交差エントロピー誤差は、正解ラベルの誤差のみを得る関数になります。
具体的には、

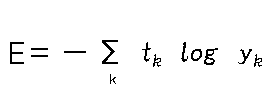
のように、正解のｔがlogの前にあるため、正解のラベル以外は０になります。（tkはone-hot表現）logは底がｅの自然対数（計算機だとln(ｙｋ)）のため、正解の１に近づくほど０になります。
またPythonで計算すると以下のようになります。正解が２の場合で、出力も２の場合は、０．５程度の誤差ですが、出力が７になると２．３程度の誤差になります。

import numpy as np
print('---交差エントロピー誤差')

def cross_entropy_error(y,t):
    delta=1e-7
    return -np.sum(t*np.log(y+delta))

#正解が２
t=[0,0,1,0,0,0,0,0,0,0]

#計算結果が２が確率が高い
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
#交差エントロピー誤差
z=cross_entropy_error(np.array(y),np.array(t))
print(z)#0.5108

#計算結果が７が確率が高い
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
#交差エントロピー誤差
z=cross_entropy_error(np.array(y),np.array(t))
print(z)#2.3025

次は交差エントロピー誤差＋ミニバッチ学習を行います。複数個の損失関数を計算できるようになります。

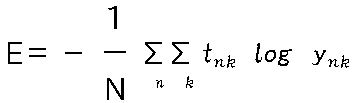
のように、ｎ個の交差エントロピー誤差の合計を計算します。
Pythonで計算すると以下のようになります。正解ラベル①は、１０個の出力があったら、[0,0,1,0,0,0,0,0,0,0,]で、正解ラベル②は[2]のようにラベルで表現した場合になります。

print('---ミニバッチ学習+交差エントロピー誤差')
import numpy as np
print('-------正解ラベル①--------')
def cross_entropy_error_v1(y,t):
    if y.ndim==1:#ｙの次元数が１
        print(y.shape)
        print(y.ndim)
        t=t.reshape(1,t.size)#次元数を２にしている（10,)→(1,10)
        y=y.reshape(1,y.size)
        print(y.shape)
        print(y.ndim)
    batch_size=y.shape[0]
    
    delta=1e-7
    print(t*np.log(y+delta))
    return -np.sum(t*np.log(y+delta))/batch_size

#正解が２ｘ３個
t=[[1,0,0,0,0,0,0,0,0,0],[0,1,0,0,0,0,0,0,0,0],[0,0,1,0,0,0,0,0,0,0]]

#計算結果が２が確率が高いｘ３個
y=[[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0],[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0],[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]]

#交差エントロピー誤差
z=cross_entropy_error_v1(np.array(y),np.array(t))

print(z)

print('-------正解ラベル②--------')
def cross_entropy_error_v2(y,t):
    if y.ndim==1:#ｙの次元数が１
        print(y.shape)
        print(y.ndim)
        t=t.reshape(1,t.size)#次元数を２にしている（10,)→(1,10)
        y=y.reshape(1,y.size)
        print(y.shape)
        print(y.ndim)
    batch_size=y.shape[0]
    delta=1e-7
    print(np.log(y[np.arange(batch_size),t]+delta))
    return -np.sum(np.log(y[np.arange(batch_size),t]+delta))/batch_size

#正解が２ｘ３個
t=0,1,2#正解がラベルであたえられた場合。t=[0,0,1,0,0,0,0,0,0,0]は２のラベル

#計算結果が２が確率が高いｘ３個
y=[[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0],[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0],[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]]

#交差エントロピー誤差
z=cross_entropy_error_v2(np.array(y),np.array(t))

print(z)

出力は以下のようになります。

---ミニバッチ学習+交差エントロピー誤差
-------正解ラベル①--------
[[-2.30258409 -0.         -0.         -0.         -0.         -0.
  -0.         -0.         -0.         -0.        ]
 [-0.         -2.99573027 -0.         -0.         -0.         -0.
  -0.         -0.         -0.         -0.        ]
 [-0.         -0.         -0.51082546 -0.         -0.         -0.
  -0.         -0.         -0.         -0.        ]]
1.9363799412166252
-------正解ラベル②--------
[-2.30258409 -2.99573027 -0.51082546]
1.9363799412166252

３個の誤差を計算した結果になります。正解ラベル①と②で、１個毎の出力は、それぞれ異なっておりますが、最終的な出力は、１．９４と同じ結果が出力されています。 np.random.choice(1000,10)のように１０００個のデータから１０個を抽出して、計算することができるようになります。
機械学習では、正解率を使って学習されているように感じますが、この誤差を小さくすることが機械学習の本質です。会社の業績を上げるために「良かった点」に着目して計画を立てがちですが、「悪かった点」に着目してその改善の計画をすすめる方が良い会社をつくる近道なのかもしれません。（機械学習で会社を運営したらきっとそうするハズです。）

－－－－－－－－－－－－－

（第４回）損失関数

＜２乗和誤差＞

＜交差エントロピー誤差＞

機械学習のメモ