マイコン君　Ｅ資格の勉強メモ

（第５回）微分（勾配算出）

誤差が算出し、それを小さくすることで良い結果が得られます。重みをどの方向に変化させれば良いか？微分を使って勾配を算出することで、決定します。計算が遅いため実用的ではありませんが、勾配をどのように算出するか理解する必要があるため、調べていきます。

＜数値微分＞

製品を作るときのサイクルタイムを短くする場合、現状が６０秒／個を一気に１０秒短縮するのは難しいですが、製品の工程を分解して、それぞれを少しずつ短縮して目標に近づけることで、目標を達成します。
同じように、機械学習でも誤差を微分して少しづつ誤差を低減していきます。まず微分の式は

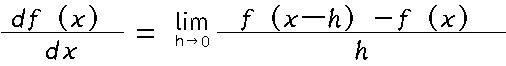
のように、関数f(x)の変化をx-hによって作り、ｈを０に近づける事で微分を行います。
しかし、Pythonで計算する場合、$1.0e^{-50}$などという数値をｈに使うと不具合が生じてしまうため、対策が必要です。

import numpy as np
print('---微分')

def function(x):
    return x**2+x

#小さすぎると扱えない
#丸め誤差
def numerical_diff(f,x):
    h=1e-50
    return (f(x+h)-f(x))/h

y=numerical_diff(function,1)
print(y)#０になってしまい、計算できていない


#丸め誤差　１ｅ－４程度なら計算できる+中心差分にする
def numerical_diff2(f,x):
    h=1e-4
    return (f(x+h)-f(x-h))/(2*h)

y=numerical_diff2(function,1)
print(y)#微分ができている

Ｐｙｔｈｏｎで計算すると$h=1.0e^{-50}$＋前方差分の方は０になってしまい、計算ができていません。しかし$h=1.0e^{-4}$程度にして、中心差分$ｆ（ｘ＋ｈ）$と$ｆ（ｘ－ｈ）$の差分にすると計算ができています。
計算結果としては、$x^{2}+x$の微分は$2x+1$ですので、numerical_diff2に$f(x)=x^{2}+x$と$ｘ＝１$を入力すると３が出力されています。

次に、$0.01x^{2}+0.1x$と$x^{2}$の２つの式のグラフを描いて、それぞれを微分してみます。ｘ＝５，１０がそれぞれ、微分した傾きになっていることが分かります。
この傾きを使って、誤差を小さくすれば良いという事になります。

import numpy as np
print('---微分の例')

def numerical_diff2(f,x):
    h=1e-4
    return (f(x+h)-f(x-h))/(2*h)

def function_l(x):
    return 0.01*x**2+0.1*x
def function_s(x):
    return x**2

import numpy as np
import matplotlib.pylab as plt

#---0.01x^2+0.1x

x=np.arange(0,20,0.1)
y=function_l(x)
plt.plot(x,y)
plt.show()

#0.01*x^2+0.1*x 微分すると-> (x+5)/50
#x=5->0.2
#x=10->0.3

ans=numerical_diff2(function_l,5)
print(ans)#０．２に近い

ans=numerical_diff2(function_l,10)
print(ans)#０．３に近い


#---x^2

x=np.arange(0,20,0.1)
y=function_s(x)
plt.plot(x,y)
plt.show()

#*x^2 微分すると-> 2x
#x=5->10
#x=10->20

ans=numerical_diff2(function_s,5)
print(ans)#10に近い

ans=numerical_diff2(function_s,10)
print(ans)#20に近い

＜偏微分＞

いままでは１つの変数の微分ですが、変数が複数になった場合も計算する必要があります。複数の変数の微分を偏微分といいますが、この傾きも算出する必要があります。

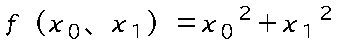
$x_0^2$と$x_1^2$をそれぞれ微分すると、$2x_{0}$、$2x_{1}$になり、ｘ０＝５、ｘ１＝１０の場合は、ｘ０の傾きが１０、ｘ１の傾きが２０という答えが得られます。
Pythonで計算する場合も、ｘ０、ｘ１それぞれ微分をすることで、同じ答えが得られます。

import numpy as np
import matplotlib.pylab as plt
print('---偏微分')

from mpl_toolkits.mplot3d import Axes3D


def numerical_diff2(f,x):
    h=1e-4
    return (f(x+h)-f(x-h))/(2*h)

def numerical_gradient_no_batch(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)
        x[idx] = tmp_val - h 
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val  # 値を元に戻す
    return grad

def function_henbibun(x):
    return x[0]**2+x[1]**2

def function_henbibun_temp1(x0):
    return x0*x0+4**2

def function_henbibun_temp2(x1):
    return 3**2+x1*x1

ans=numerical_diff2(function_henbibun_temp1,5)
print(ans)#ｘ０で微分
ans=numerical_diff2(function_henbibun_temp2,10)
print(ans)#ｘ１で微分

x0=5.
x1=10.
X=[x0,x1]
ans=numerical_gradient_no_batch(function_henbibun,np.array(X))
print(ans)#ｘ０、ｘ１別々に微分したときと同じ結果

x0=np.arange(-5,5,0.1)
x1=np.arange(-10,10,0.2)
X=[x0,x1]

X=np.meshgrid(x0,x1)
for i in X:
    y = function_henbibun(X)
    #plt.plot(i, y)
    #plt.show()#ｘ軸はi=0がx0、i=1がx1の方向のグラフ
    
fig = plt.figure()
ax = Axes3D(fig)
y = function_henbibun(np.array([X[0], X[1]]))
ax.plot_wireframe(X[0], X[1], y)

plt.show()

Ｐｙｔｈｏｎを実行すると、偏微分の計算ができます。ｘ０：－５．０～５．０、ｘ１：１０．０～１０．０のグラフを描いて、ｘ０＝５、ｘ＝１０の部分がｘ０の傾きが１０、ｘ１の傾きが２０になっていることがわかります。（Ｐｙｔｈｏｎのグラフウィンドウではグラフが回転できます）

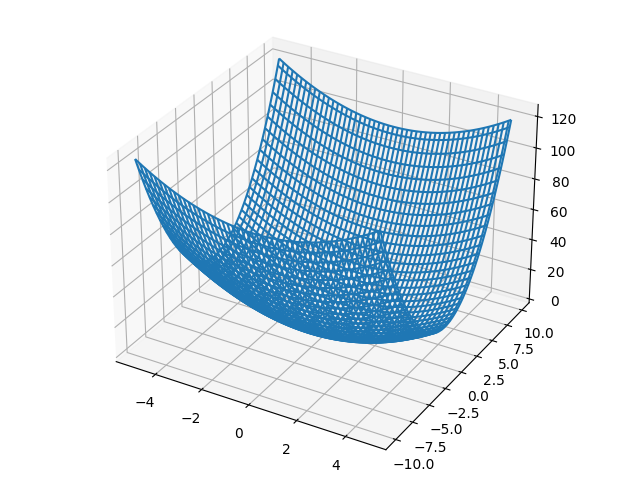
＜勾配＞

偏微分のグラフをみると、ある方向に進むことで、中央に近づくことがわかりますが、実際に方向を数値化するためにＰｙｔｈｏｎで計算します。

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D


def _numerical_gradient_no_batch(f, x):
    h = 1e-4  
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)
        x[idx] = tmp_val - h 
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val  # 値を元に戻す
    return grad

def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        return grad


def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)
    
if __name__ == '__main__':
    print("勾配")

    x0 =np.arange(-5,5.5,1)
    x1=np.arange(-10,10.5,1)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()
    
    mytest=numerical_gradient(function_2, np.array([X, Y]).T).T
    grad = mytest#これが勾配の配列になる。

    plt.figure()
    #plt.scatter(X, Y, s=10, color='red')#出力座標
    plt.quiver(X, Y, -grad[0], -grad[1],  angles='xy', color="#666666")
    #X, Y:ベクトルの開始点
    #-grad[0], -grad[1]はベクトルの成分


    plt.xlim([-5, 5])
    plt.ylim([-5, 5])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.draw()
    plt.show()

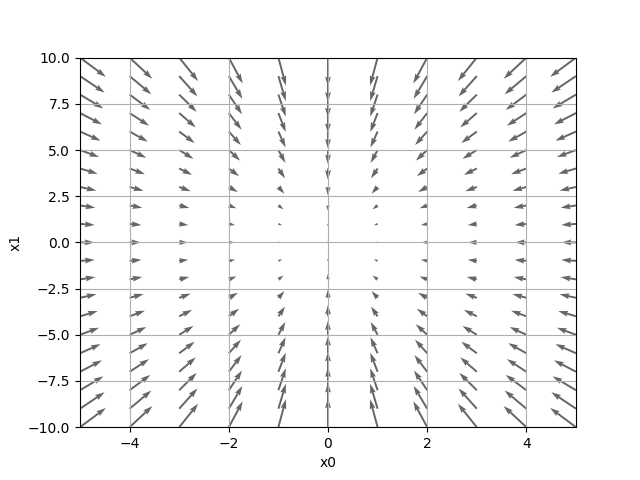
偏微分で出力した図の傾きを考えると上の図のようになると思います。この傾きの方向に進めれば、誤差を小さくできそうです。

＜勾配法＞

いよいよ誤差の傾きを小さくするために、パラメーターを変更して目標にむかって変更させます。勾配の方向へ進める方法を勾配法といい、１回の更新量を学習率と呼びます。
実際にPythonで計算すると次の通りになります。学習率が０．１の場合は、（０，０）に向かって進むのですが、学習率が１０（大きすぎ）や、 $1e^{-10}$（小さすぎ）など適切でない学習率の場合は、目標に進まないことがわかります。

import numpy as np
import matplotlib.pylab as plt


print("勾配法")
def _numerical_gradient_no_batch(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)
        x[idx] = tmp_val - h 
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val  # 値を元に戻す
    return grad


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)

        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
            
        return grad
    
def gadien_descenf(f,init_x,lr=0.01,step_num=100):
    x=init_x

    for i in range(step_num):
        grad=numerical_gradient(f,x)
        x-= lr *grad
    return x

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)

def function_2(x):
    return x[0]**2+x[1]**2

init_x=np.array([5.,10.])#正しく計算できそう（０，０）へ向かっている
ans=gadien_descenf(function_2,init_x=init_x,lr=0.1,step_num=100)
print(ans)

init_x=np.array([5.,10.])#学習率が大きすぎて、発散している
ans=gadien_descenf(function_2,init_x=init_x,lr=10,step_num=100)
print(ans)

init_x=np.array([5.,10.])#学習率が小さすぎて、同じ位置（５，１０）のまま
ans=gadien_descenf(function_2,init_x=init_x,lr=1e-10,step_num=100)
print(ans)

#図を描く
init_x = np.array([5., 10.0])    

lr =0.1
step_num = 100
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)

plt.plot( [-10, 10], [0,0], '--b')
plt.plot( [0,0], [-10, 10], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')

plt.xlim(-5, 5)
plt.ylim(-10 ,10)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()

適切な学習率で計算すると、外側の点から、中央（０，０）の方向に値が更新されていくことが下の図で分かります。

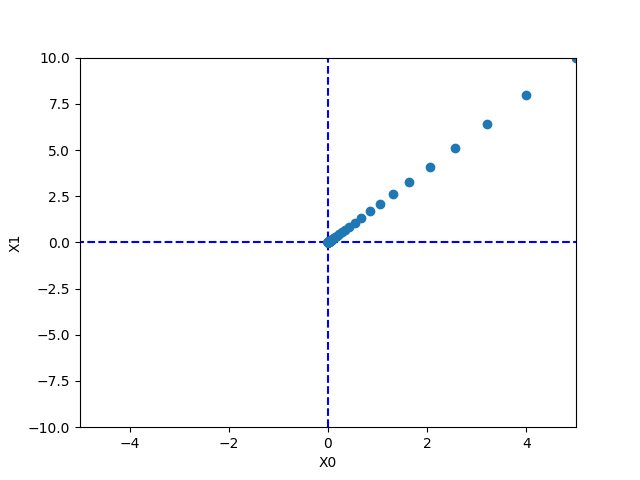
微分をすることで、傾きを求め、その傾きの方向に値を更新することで、目標の数値に近づくことがわかりました。

－－－－－－－－－－－－－

（第５回）微分（勾配算出）

＜数値微分＞

＜偏微分＞

＜勾配＞

＜勾配法＞

機械学習のメモ