マイコン君　Ｅ資格の勉強メモ

（第９回）パラメータの更新（最適化）

損失関数の値を小さくするために学習を行うのですが、効率よくパラメータを見つける必要があります。これを最適化と言い、学習率やいままで調べた確率的勾配降下法（ＳＧＤ）以外にも色々な方法があります。

＜関数＞

これから進める方法は、以下の関数の最小値を求めることを目標としてすすめます。
$\Large{f(x,y)＝\frac{1}{20}x^{2}+y^{2}}$
この関数をグラフにする場合は、このプログラムのとおりになります。

＜ＳＧＤ＞

ＳＧＤは確率的勾配降下法という手法になります。これまではこの方法を使っていましたが、簡単であるため欠点があります。

$\Large{W←W-η\frac{∂L}{∂W}}$

「←」は値を更新するという意味で、重みのパラメーターを「学習率（η）×勾配（∂L/∂W）」を引き算しながらパラメーターを更新して行きます。
プログラムは以下のとおり

import sys, os
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):#上の微分
    return x / 10.0, 2.0*y

class SGD:

    """確率的勾配降下法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key] 



init_pos = (10.0, 5.0)#初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0,0
optimizers = OrderedDict()
optimizers["SGD_lr=0.95"] = SGD(lr=0.95)
optimizers["SGD_lr=0.75"] = SGD(lr=0.75)
optimizers["SGD_lr=0.55"] = SGD(lr=0.55)
optimizers["SGD_lr=0.35"] = SGD(lr=0.35)

idx = 1
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(50):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])#微分を計算（傾き）
        optimizer.update(params, grads)
    
    print(key,format(params['x'], '.4f'),format(params['y'], '.4f'))
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)#等高線用Z
    
    # for simple contour line  
    mask = Z > 5
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, '.-', color="red")
    plt.contour(X, Y, Z)#等高線
    plt.ylim(-5, 5)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.title(key, x=.5, y=0)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

実行すると以下のグラフが作成されます。

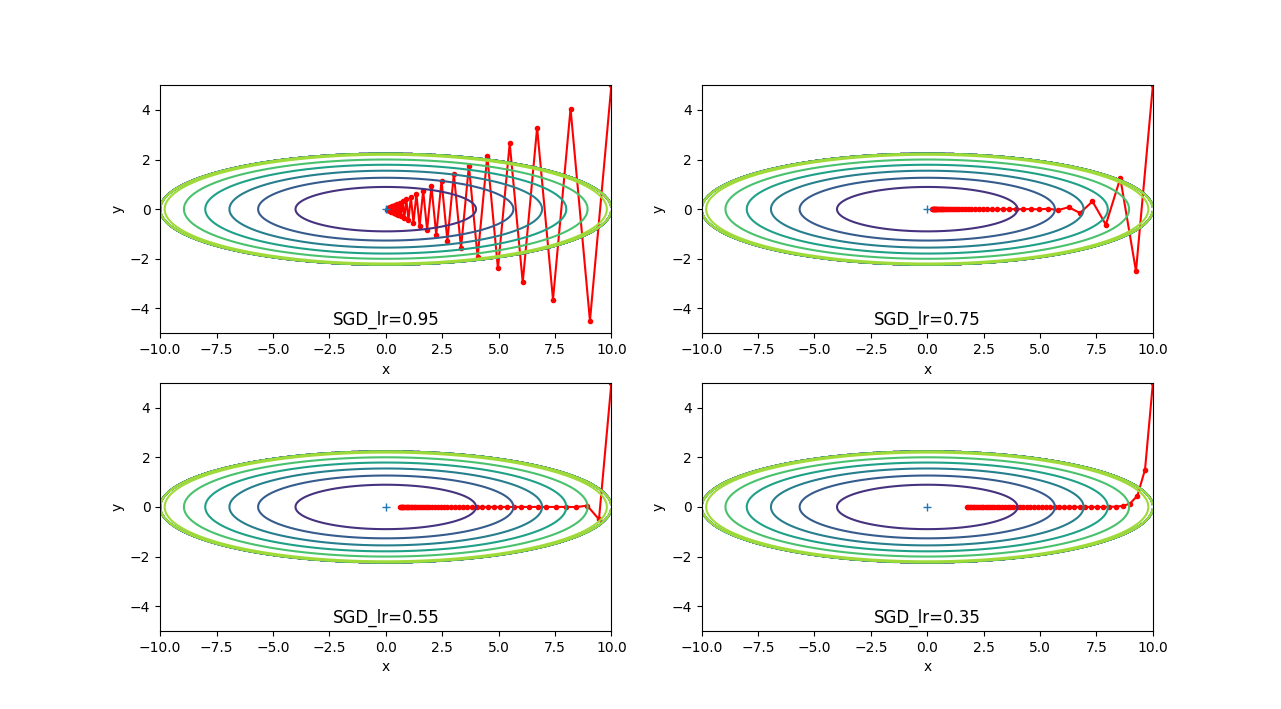
５０回パラメータを更新して最小値を目標にすすみますが、学習率が低くなると、中央に到達していないことがわかります。学習率が大きいと中央に到達できますが、ギザギザが大きくなり効率が悪い事が分かります。ｙとｘの傾きの大きさが２０倍違うため、ギザギザになってしまいます。

＜Momentum＞

Momentumはすり鉢にいれたボールが中央に転がるような動きをする方法です

$\Large{v←αv-η\frac{∂L}{∂W}}$
$\Large{W←W+v}$

ｖという変数が追加され、αvによって、変化量が小さいｘ方向もしっかりパラメータが更新されるようになります。
プログラムは以下のとおり

import sys, os
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):#上の微分
    return x / 10.0, 2.0*y

class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]


init_pos = (10.0, 5.0)#初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0,0
optimizers = OrderedDict()
optimizers["Momentum_lr=0.1"] = Momentum(lr=0.1)
optimizers["Momentum_lr=0.08"] = Momentum(lr=0.08)
optimizers["Momentum_lr=0.06"] = Momentum(lr=0.06)
optimizers["Momentum_lr=0.04"] = Momentum(lr=0.04)

idx = 1
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(70):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])#微分を計算（傾き）
        optimizer.update(params, grads)
    
    print(key,format(params['x'], '.4f'),format(params['y'], '.4f'))
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)#等高線用Z
    
    # for simple contour line  
    mask = Z > 5
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, '.-', color="red")
    plt.contour(X, Y, Z)#等高線
    plt.ylim(-5, 5)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.title(key, x=.5, y=0)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

実行すると以下のグラフが作成されます。

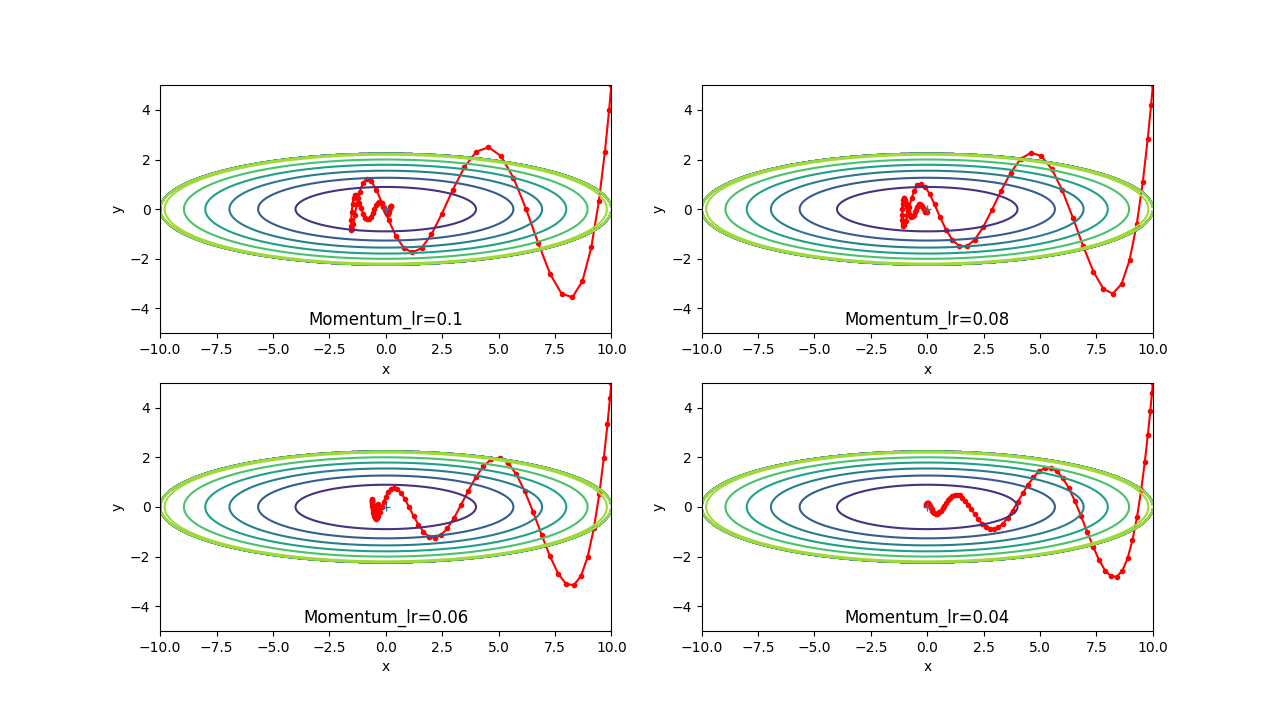
７０回パラメータを更新しています。学習率が０．１では、通り過ぎて戻り、０．０４では直接中央に到達しています。ボールが中央ような動きになっています。αは０．９に設定していますが数値を変更すると到達しなくなったりします。

＜ＡｄａＧｒａｒｄ＞

ＡｄａＧｒａｒｄは学習率ηを固定ではなく、変化させる方法です。学習率を減衰させることで、最初は大きく、徐々に小さくすることで、効率よくパラメータの更新を行います。

$\Large{h←h+\frac{∂L}{∂W}⦿\frac{∂L}{∂W}}$
$\Large{W←W-η\frac{1}{\sqrt{h}}\frac{∂L}{∂W}}$

⦿は行列の要素ごとの掛け算を意味しており、勾配の２乗和として、ｈという変数にします。
$\frac{1}{\sqrt{h}}$を掛け算することで、大きく変化した要素の学習率が小さくなるようになります。
プログラムは以下のとおり

import sys, os
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):#上の微分
    return x / 10.0, 2.0*y

class AdaGrad:

    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


init_pos = (10.0, 5.0)#初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0,0
optimizers = OrderedDict()
optimizers["AdaGrad_lr=3.0"] = AdaGrad(lr=3.0)
optimizers["AdaGrad_lr=1.5"] = AdaGrad(lr=1.5)
optimizers["AdaGrad_lr=1.2"] = AdaGrad(lr=1.0)
optimizers["AdaGrad_lr=0.9"] = AdaGrad(lr=0.5)

idx = 1
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(50):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])#微分を計算（傾き）
        optimizer.update(params, grads)
    
    print(key,format(params['x'], '.4f'),format(params['y'], '.4f'))
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)#等高線用Z
    
    # for simple contour line  
    mask = Z > 5
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, '.-', color="red")
    plt.contour(X, Y, Z)#等高線
    plt.ylim(-5, 5)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.title(key, x=.5, y=0)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

実行すると以下のグラフが作成されます。

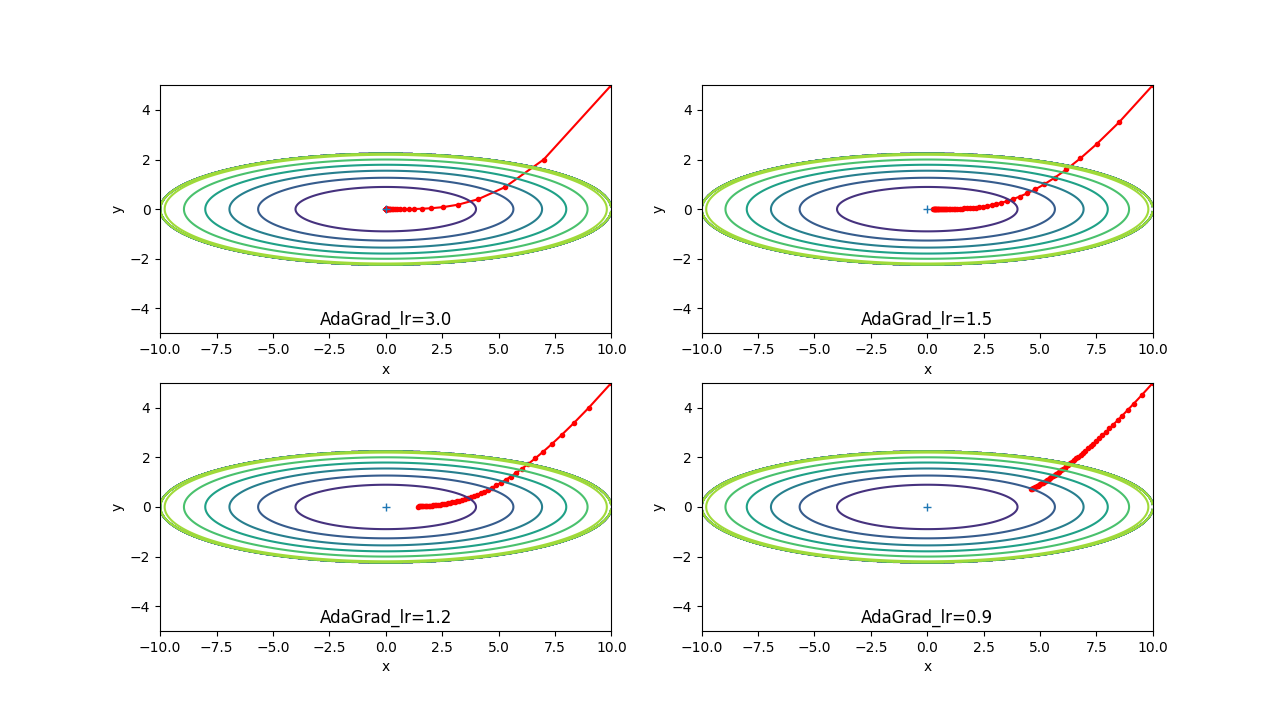
５０回パラメータを更新しています。学習率が３．０で直接中央に到達していますが、学習率の初期が低いと中央に到達していません。しかし、どの学習率でも同じような形になるので、回数を多くすれば、結果的に同じ用なモデルが作成されると予想できます。

＜ＲＭＳｐｒｏｐ＞

ＲＭＳｐｒｏｐはＡｄａＧｒａｒｄの学習率を０にならないようにする方法です。ＡｄａＧｒａｒｄは学習が進むと、学習率ηが減衰し続けて、最終的には０に近くなり、学習が進まなくなってしまいます。最新の勾配の情報が大きく反映され、過去の勾配情報の影響を小さくします。

$\Large{h←hβ+(1-β)\frac{∂L}{∂W}⦿\frac{∂L}{∂W}}$
$\Large{W←W-η\frac{1}{\sqrt{h}}\frac{∂L}{∂W}}$

ＡｄａＧｒａｒｄにβという変数が加わり、ｈβ、（１－β）によって、ｈが直近と過去の勾配の影響の度合いを調整しています。
プログラムは以下のとおり

import sys, os
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):#上の微分
    return x / 10.0, 2.0*y

class RMSprop:

    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)



init_pos = (10.0, 5.0)#初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0,0
optimizers = OrderedDict()
optimizers["RMSprop_lr=0.45"] = RMSprop(lr=.45)
optimizers["RMSprop_lr=0.35"] = RMSprop(lr=.35)
optimizers["RMSprop_lr=0.25"] = RMSprop(lr=.25)
optimizers["RMSprop_lr=0.15"] = RMSprop(lr=.15)

idx = 1
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(50):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])#微分を計算（傾き）
        optimizer.update(params, grads)
    
    print(key,format(params['x'], '.4f'),format(params['y'], '.4f'))
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)#等高線用Z
    
    # for simple contour line  
    mask = Z > 5
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, '.-', color="red")
    plt.contour(X, Y, Z)#等高線
    plt.ylim(-5, 5)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.title(key, x=.5, y=0)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

実行すると以下のグラフが作成されます。

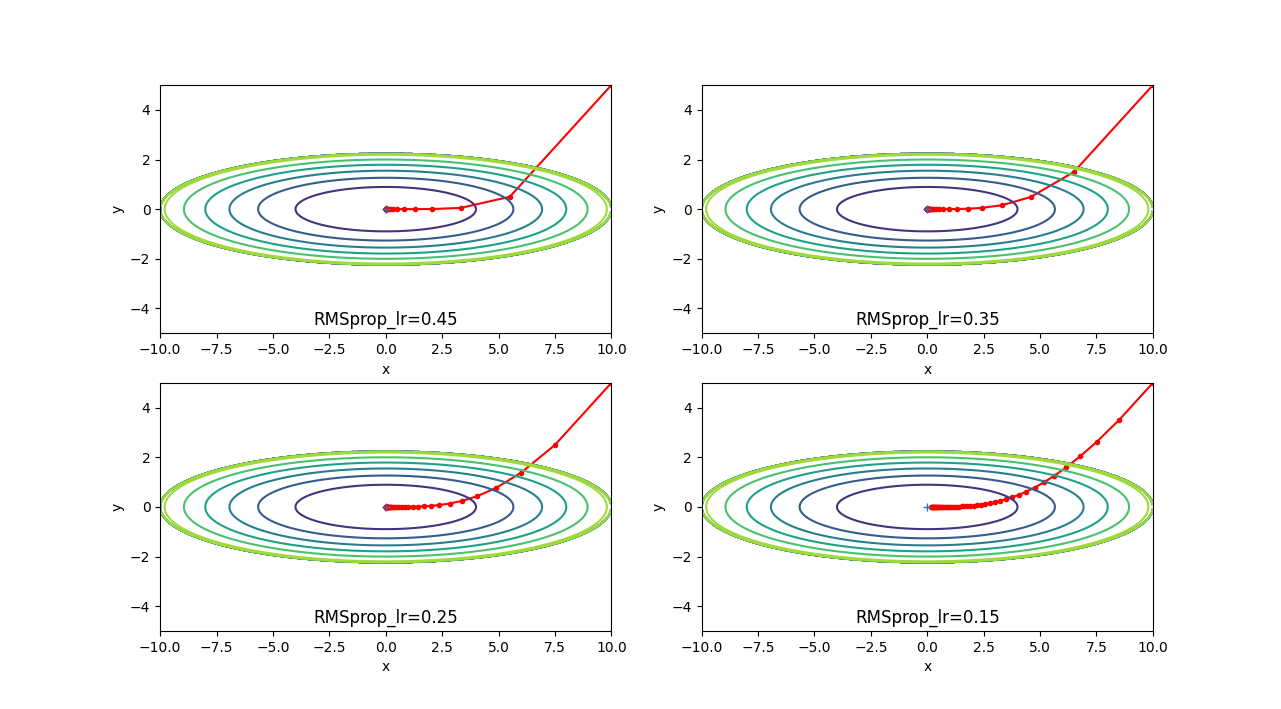
５０回パラメータを更新しています。学習率が０．５を超えるとあまりよくなさそうな更新の挙動ですが、基本的には、ＡｄａＧｒａｒｄと同じような更新の挙動になっています。

＜Ａｄａｍ＞

ＡｄａｍはＡｄａＧｒａｒｄ＋Ｍｏｍｅｎｔｕｍの手法です。

$\Large{m←(1-β_{1})(\frac{∂L}{∂W}-m)}$
$\Large{v←(1-β_{2})(\frac{∂L}{∂W}⦿\frac{∂L}{∂W}-v)}$
$\Large{W←W-η\frac{m}{\sqrt{v}+10^{-7}}}$
学習率η、$β_{1}$、$β_{2}$の３つのハイパーパラメータを設定としています。標準的には $β_{1}$＝０．９、$β_{2}$＝０．９９９のようです。

プログラムは以下のとおり

import sys, os
#sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
#from optimizer import *

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):#上の微分
    return x / 10.0, 2.0*y

class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)


init_pos = (10.0, 5.0)#初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0,0
optimizers = OrderedDict()
optimizers["Adam_lr=3.0"] = Adam(lr=3.0)
optimizers["Adam_lr=1.5"] = Adam(lr=1.5)
optimizers["Adam_lr=1.0"] = Adam(lr=1.0)
optimizers["Adam_lr=0.5"] = Adam(lr=0.5)
#optimizers["Momentum"] = Momentum(lr=0.1)
#optimizers["AdaGrad"] = AdaGrad(lr=1.5)
#optimizers["Adam"] = Adam(lr=0.3)

idx = 1
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(50):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])#微分を計算（傾き）
        optimizer.update(params, grads)
    
    print(key,format(params['x'], '.4f'),format(params['y'], '.4f'))
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)#等高線用Z
    
    # for simple contour line  
    mask = Z > 5
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, '.-', color="red")
    plt.contour(X, Y, Z)#等高線
    plt.ylim(-5, 5)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.title(key, x=.5, y=0)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

実行すると以下のグラフが作成されます。

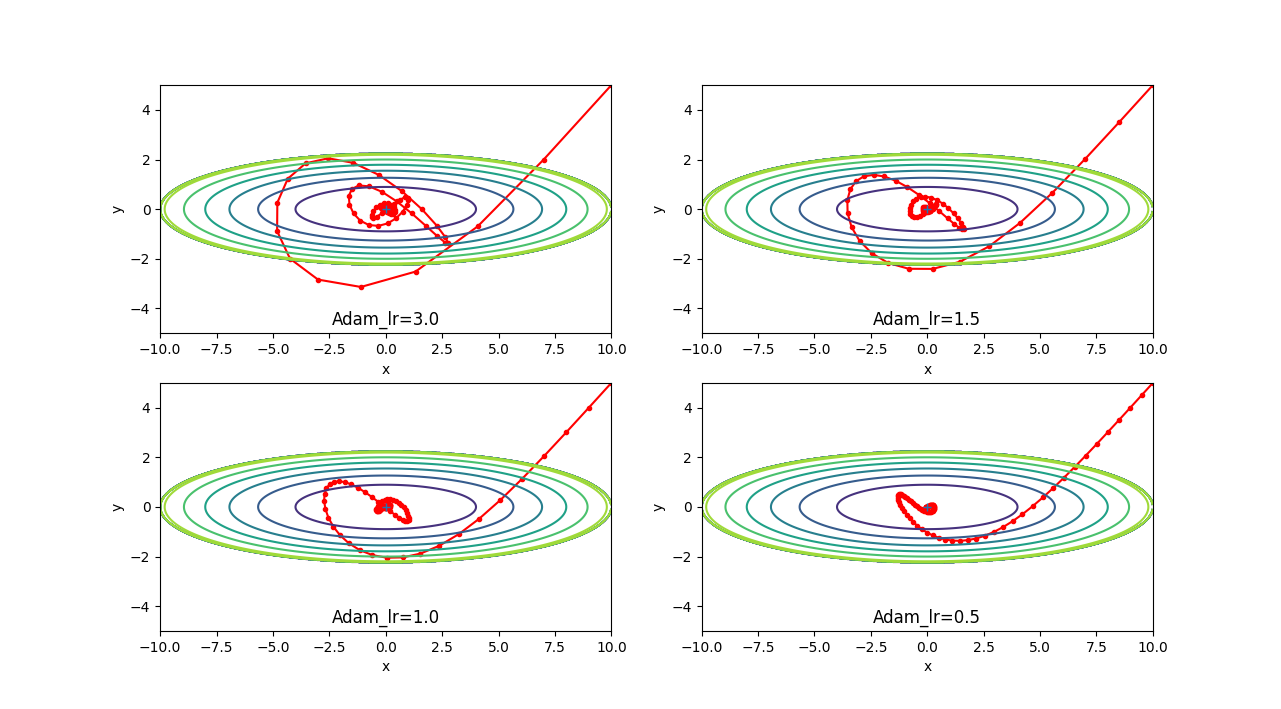
１００回パラメータを更新しています。どの学習率でも中央に向かおうという意思のようなものがあり、これが良さそうと感じますが、実際はこれが優秀という事はなく、どんなデータか？どの手法を使うか？によって、変わるようです。

＜比較＞

いままでの手法を２０００回学習したときの誤差を比較します。Nesterovの加速法も加えて、比較します。

以下のプログラムをダウンロードして保存します。MNISTのデータセットも必要なので、展開済みの「mnist.pkl」も同じフォルダに保存しておきます。
mnist.py
multi_layer_net.py
optimizer.py
util.py

プログラムは以下のとおり

# coding: utf-8
import os
import sys
import matplotlib.pyplot as plt
from mnist import load_mnist
from util import smooth_curve
from multi_layer_net import MultiLayerNet
from optimizer import *
import pickle

# 0:MNISTデータの読み込み==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:実験の設定==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
optimizers['RMSprop'] = RMSprop()
optimizers['Nesterov'] = Nesterov()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:訓練の開始==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    for key in optimizers.keys():   
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.グラフの描画==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "RMSprop": "D", "Nesterov": "o", "Adam": "x"}
x = np.arange(max_iterations)


  
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
    print(key)
    techacademy = networks[key]
    with open('MyNetwork_' + key +'.pkl', 'wb') as MyNetwork:
        pickle.dump(techacademy , MyNetwork)
    #for idx in range(1, networks[key].hidden_layer_num+2):
    #    print('No'+str(idx))
    #    print(networks[key].params['W'+ str(idx)].shape)
    #    print(networks[key].params['b'+ str(idx)].shape)
    
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

実行すると以下のグラフが作成されます。

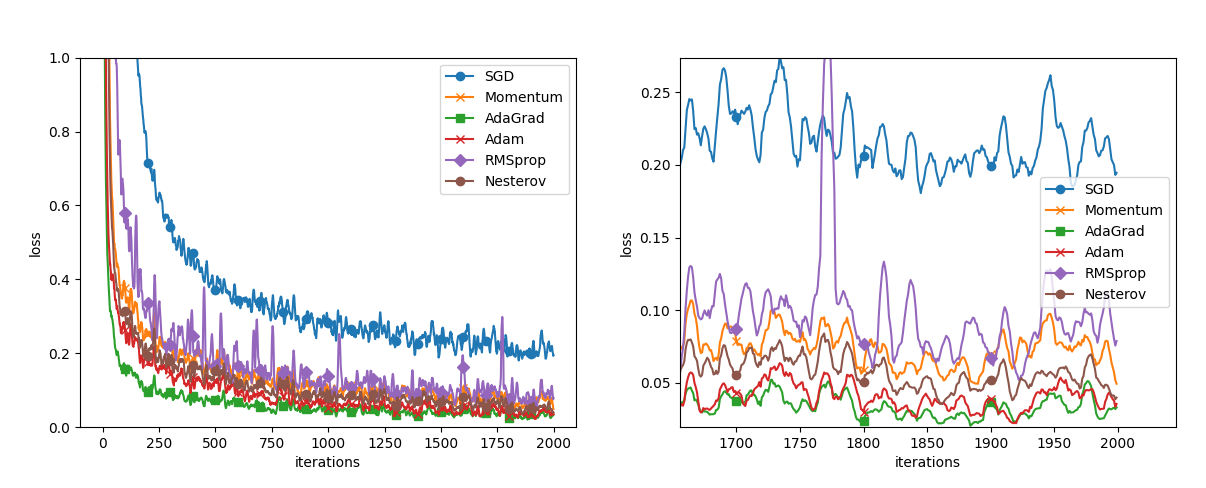
MNISTのモデルの学習を２０００回計算したときの誤差のグラフです。最後の方を拡大すると、ＡｄａＧａｒｄが良さそうに見えますが、学習率などでも異なるので、一概には言えません。しかし手法によって差異が生まれるという事を考えて学習をさせる必要があるという事なんだろうと思います。
また、出力された後に、各手法のファイルが生成されます。これはモデルファイルとなっており、読みだせば、手書きの文字を認識させることも可能です。同じフォルダに手書きをした「test.png」のファイルを準備して実行すると判別できます。

# coding: utf-8
import os
import sys
import matplotlib.pyplot as plt
from optimizer import *
import pickle
from PIL import Image

#モデルを読みだす
with open('MyNetwork_SGD.pkl', 'rb') as  MyNetwork:
  MyNetwork_Model = pickle.load( MyNetwork)

#自分で書いた文字を表示
myimg = Image.open('test.png').convert('L')
myimg.thumbnail((28, 28)) # 28*28に変換
myimg = np.array(myimg) # numpy arrayに変換
plt.imshow(myimg)
plt.show()

#自分で書いた文字を判定
myimg_array=np.array(myimg.flatten())
myimg_array=myimg_array/255
myimg_array=myimg_array.reshape(1,784)
print(myimg_array.shape)

y = MyNetwork_Model.predict(myimg_array)
print(y)
p=np.argmax(y)
print(p)

－－－－－－－－－－－－－

（第９回）パラメータの更新（最適化）

＜関数＞

＜ＳＧＤ＞

＜Momentum＞

＜ＡｄａＧｒａｒｄ＞

＜ＲＭＳｐｒｏｐ＞

＜Ａｄａｍ＞

＜比較＞

機械学習のメモ